题目内容
12.解不等式组:(1)$\left\{\begin{array}{l}{2x+3≥x+11}\\{\frac{2x+5}{3}-1<2-x}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x}\\{x-1≤\frac{3}{4}x-\frac{1}{8}}\end{array}\right.$.
分析 (1)根据解不等式的步骤先求出两个不等式的解集,再在数轴上表示出来,然后找出解集的公共部分即可;
(2)先求出两个不等式的解集,再在数轴上表示出来,然后找出解集的公共部分即可;
解答 解:(1)$\left\{\begin{array}{l}{2x+3≥x+11①}\\{\frac{2x+5}{3}-1<2-x②}\end{array}\right.$,
由①得:x≥8,
由②得:x<$\frac{4}{5}$,
在数轴上可表示为:
则原不等式组的解集是无解;
(2)$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x①}\\{x-1≤\frac{3}{4}x-\frac{1}{8}②}\end{array}\right.$,
由①得:x>-$\frac{12}{5}$,
由②得:x≤7,
则原不等式组的解集是-$\frac{12}{5}$<x≤7.
点评 本题考查了不等式组的解集:几个不等式组成的不等式组的解集为这几个不等式的解集的公共部分.

练习册系列答案
相关题目
20.已知函数y=2x+5,当自变量x增加m时,相应的函数值将增加( )
| A. | 2m+1 | B. | 2m | C. | m | D. | 2m-1 |
17.方程x2-(m+6)x+m2=0有两个相等的实数根,则m的值是( )
| A. | -2或6 | B. | 6 | C. | -2 | D. | -6或2 |
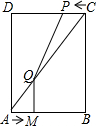 如图,在矩形ABCD中,AD=2DC=4,动点M以每秒1个单位的长度的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿线段CD向点D运动.当点M到达点B时,两点同时停止运动.过点M作QM⊥AB于点M交AC于点Q,连接QP.若点M运动的时间为t(秒).
如图,在矩形ABCD中,AD=2DC=4,动点M以每秒1个单位的长度的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿线段CD向点D运动.当点M到达点B时,两点同时停止运动.过点M作QM⊥AB于点M交AC于点Q,连接QP.若点M运动的时间为t(秒).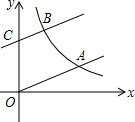 如图,一次函数y=$\frac{1}{3}$x的图象与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点A,将一次函数y=$\frac{1}{3}$x的图象向上平移3个单位得到一次函数y=ax+b的图象,它与y轴交于点C,与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点B,已知OA=2BC.
如图,一次函数y=$\frac{1}{3}$x的图象与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点A,将一次函数y=$\frac{1}{3}$x的图象向上平移3个单位得到一次函数y=ax+b的图象,它与y轴交于点C,与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于点B,已知OA=2BC.