Question

如图，过边长为2的正方形ABCD的中心O引两条互相垂直的射线，分别与正方形的边交于E，F两点，则线段EF长的取值范围是（　　）

• A、

  2

  ≤EF≤2
• B、

  2

  2

  ≤EF≤2

  2

• C、

  2

  ≤EF≤2

  2

• D、

  2

  2

  ≤EF≤

  2

Answer 1

考点：全等三角形的判定与性质,正方形的性质

专题：

分析：如图，作辅助线；证明△AOE≌△DOF，进而得到OE=OF，此为解决该题的关键性结论；求出OE的范围，借助勾股定理即可解决问题．

解答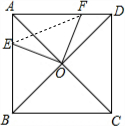：解：如图，连接EF；
∵四边形ABCD为正方形，
∴∠EAO=∠FDO=45°，AO=DO；
∵∠EOF=90°，∠AOD=90°，
∴∠AOE=∠DOF；
在△AOE与△DOF中，

∠EAO=∠FDO AO=DO ∠AOE=∠DOF

，
∴△AOE≌△DOF（SAS），
∴OE=OF（设为λ）；
由勾股定理得：
EF²=OE²+OF²=2λ²；
由题意可得：1≤λ≤

2

，
∴

2

≤EF≤2，
故选A．

点评：该题以正方形为载体，主要考查了正方形的性质、全等三角形的判定等几何知识点的应用问题；牢固掌握全等三角形的判定等几何知识点，是灵活解题的基础和关键．