题目内容
3.一组代数式:-$\frac{{a}^{2}}{2}$,$\frac{{a}^{3}}{5}$,-$\frac{{a}^{4}}{10}$,$\frac{{a}^{5}}{17}$…,观察规律,则第10个代数式是$\frac{{a}^{11}}{101}$.分析 根据分子的变化规律可知,第10个代数式的分子为a11,分母为102+1,符号为正,可得结果.
解答 解:∵-$\frac{{a}^{2}}{2}$,$\frac{{a}^{3}}{5}$,-$\frac{{a}^{4}}{10}$,$\frac{{a}^{5}}{17}$…,
∴第10项分子为a10+1=a11,
第10项分母为102+1=101,
第10项符号为“+”,
∴第10个代数式为$\frac{{a}^{11}}{101}$.
故答案为:$\frac{{a}^{11}}{101}$.
点评 本题主要考查了单项式的变化规律,发现分子分母与项数的关系是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
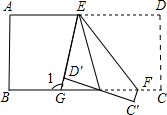 如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=50°,则∠1=100°.
如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=50°,则∠1=100°.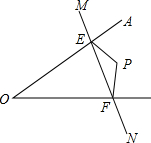 如图所示,点P在∠AOB内部,点M、N分别是点P关于AO、BO的对称点,若△PEF的周长为13cm,ME=3cm,FN=4cm,则EF=6cm.
如图所示,点P在∠AOB内部,点M、N分别是点P关于AO、BO的对称点,若△PEF的周长为13cm,ME=3cm,FN=4cm,则EF=6cm.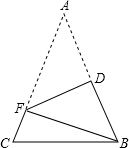 如图,在△ABC中,AB=AC,AB+BC=8,将△ABC折叠,使点A落在点B处,折痕为DF,则△BCF的周长是( )
如图,在△ABC中,AB=AC,AB+BC=8,将△ABC折叠,使点A落在点B处,折痕为DF,则△BCF的周长是( ) 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC 分别交于点G,F,H为CG的中点,连结DE、EH、DH、FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若$\frac{AE}{AB}$=$\frac{2}{3}$,则$\frac{{S}_{△DHC}}{{S}_{△EDH}}$=$\frac{3}{13}$.其中结论正确的有( )
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC 分别交于点G,F,H为CG的中点,连结DE、EH、DH、FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若$\frac{AE}{AB}$=$\frac{2}{3}$,则$\frac{{S}_{△DHC}}{{S}_{△EDH}}$=$\frac{3}{13}$.其中结论正确的有( )