题目内容
18.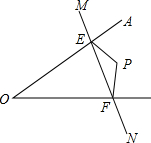 如图所示,点P在∠AOB内部,点M、N分别是点P关于AO、BO的对称点,若△PEF的周长为13cm,ME=3cm,FN=4cm,则EF=6cm.
如图所示,点P在∠AOB内部,点M、N分别是点P关于AO、BO的对称点,若△PEF的周长为13cm,ME=3cm,FN=4cm,则EF=6cm.
分析 根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长,于是得到结论.
解答 解:∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于13cm,
∴MN=13cm,
∵ME=3cm,FN=4cm,
∴EF=6cm,
故答案为:6.
点评 本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
8.下列计算①(-1)0=-1;②(-1)-1=-1;③2×2-2=$\frac{1}{2}$;④3a-2=$\frac{1}{{3a}^{2}}$;⑤(-a2)m=(-am)2.正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.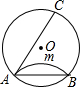 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
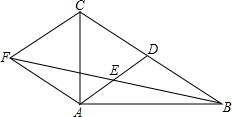 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.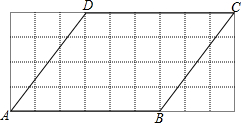 如图,在4×9的方格图中,?ABCD的顶点均在格点上,按下列要求作图:
如图,在4×9的方格图中,?ABCD的顶点均在格点上,按下列要求作图: