题目内容
14.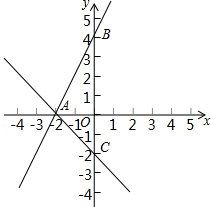 如图,一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),且与y轴分别交于B、C两点,则△ABC的面积为6.
如图,一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0),且与y轴分别交于B、C两点,则△ABC的面积为6.
分析 将点A(-2,0)分别代入两直线解析式求得a、b的值,即可得点B、C的坐标,再根据面积公式求解可得.
解答 解:将点A(-2,0)代入y=2x+a,得:-4+a=0,
解得:a=4,
∴一次函数y=2x+4与y轴的交点B的坐标为(0,4),
将点A(-2,0)代入y=-x+b,得:2+b=0,
解得:b=-2,
∴一次函数y=x-2与y轴的交点C坐标为(0,-2),
则△ABC的面积为$\frac{1}{2}$×6×2=6,
故答案为:6.
点评 本题主要考查待定系数法求函数解析式,掌握函数图象的交点坐标满足每个函数的解析式是解题的关键.

练习册系列答案
相关题目
4.下列每组数分别表示三根木棒的长度,首尾顺次相接可以构成直角三角形的一组是( )
| A. | 4,5,6 | B. | 1.5,2,2.5 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,3 |
2.某工厂二月份的产值比一月份的产值增长了x%,三月份的产值又比二月份的产值增长了x%,则三月份的产值比一月份的产值增长了( )
| A. | 2x% | B. | 1+2x% | C. | (1+x%)x% | D. | (2+x%)x% |
9.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a6-a2=a4 | C. | (a2)3=a6 | D. | (a+1)2=a2+1 |
19.若a2-b2=-$\frac{1}{16}$,a+b=-$\frac{1}{4}$,则a-b的值为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 2 | D. | 4 |
6.下列计算正确的是( )
| A. | 2+a=2a | B. | 2a-3a=-1 | C. | (-a)2•a3=a5 | D. | 8ab÷4ab=2ab |
4. 有理数a、b在数轴上的位置如图所示,下列各式成立的是( )
有理数a、b在数轴上的位置如图所示,下列各式成立的是( )
 有理数a、b在数轴上的位置如图所示,下列各式成立的是( )
有理数a、b在数轴上的位置如图所示,下列各式成立的是( )| A. | b>0 | B. | |a|>一b | C. | a+b>0 | D. | ab<0 |
