题目内容
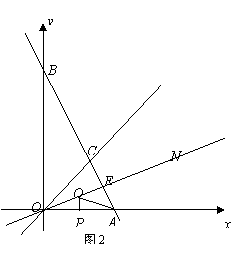
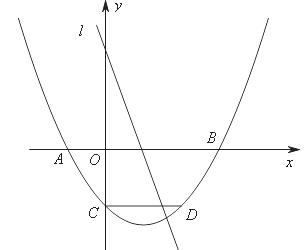
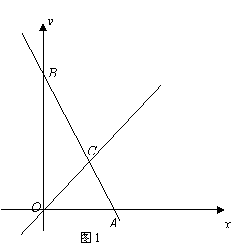
如图,抛物线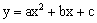 关于直线
关于直线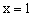 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D 在抛物线上,直线
在抛物线上,直线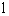 是一次函数
是一次函数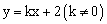 的图象,点O是坐标原点。
的图象,点O是坐标原点。
(1)求抛物线的解析式;
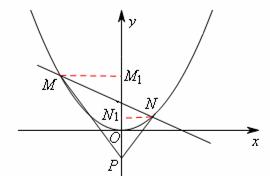
(2)把抛物线向左平移1个单位,再向上平移4个单位,所得抛物线与直线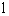 交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴
交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴 对称?若存在,求出P点坐标;若不存在,请说明理
对称?若存在,求出P点坐标;若不存在,请说明理 由.
由.
(1)∵抛物线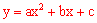 关于直线x=1对称,AB=4,∴A(-1,0),B(3,0) 。
关于直线x=1对称,AB=4,∴A(-1,0),B(3,0) 。
∴可设抛物线的解析式为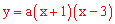
 。
。
∵点D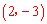 在抛物线上,∴
在抛物线上,∴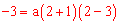 ,解得
,解得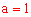 。
。
∴抛物线的解析式为 ,即
,即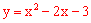 。
。
(2)∵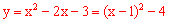 ,
,
∴把抛物线向左平移1个单位,再向上平移4个单位,所得抛物线的解析式为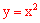 。
。
假设在y轴上存在一点P(0,t),t<0,使直线PM与PN关于y轴对称,过点M、N分别向y轴作垂线MM1、NN1,垂足分别为M1、N1,
∵∠MPO=∠NPO,∴Rt△MPM1∽Rt△NPN1。
∴ ………①。
………①。
不妨设M(xM,yM)在点N(xN,yN)的左侧,
因为P点在y轴负半轴上,则①式变为 。
。
又∵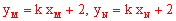 ,
,
∴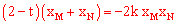 ………②。
………②。
把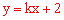 代入
代入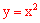 中,整理得
中,整理得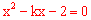 。
。
∴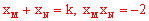 ,代入②得
,代入②得
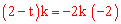 ,解得
,解得 ,符合条件。
,符合条件。
∴在y轴负半轴上存在一点P(0,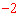 ),
), 使直线PM与PN总是关于y轴对称。
使直线PM与PN总是关于y轴对称。
【考点】二次函数综合题,平移和轴对称问题,待定系数法的应用,曲线上点的坐标与方程的关系,二次函数的性质,一元二次方程根与系数的关系。


练习册系列答案
相关题目
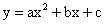
 过点B。
过点B。 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。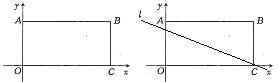
 B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )
B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )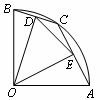

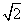
 D.
D.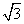

 两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】
两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【 】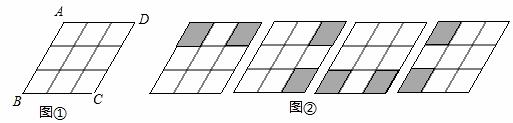
 OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m=
OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E,当△ADE是等腰直角三角形时,m= ,点E的坐标为 ;
,点E的坐标为 ;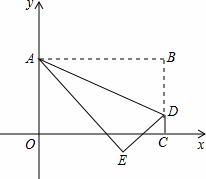

 旋转45
旋转45 方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;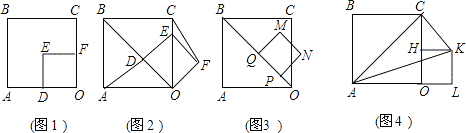

 轴交于点A
轴交于点A ,与
,与 轴交于点B,与直线OC:
轴交于点B,与直线OC: 交于点C.
交于点C.

 ,
, 的平分线ON,若AB⊥ON,垂足为E, OA=4
的平分线ON,若AB⊥ON,垂足为E, OA=4 ,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.