题目内容
如图,菱形ABCD中,边长为2,∠B=60°,将△ACD绕点C旋转,当AC(即A′C)与AB交于一点E,CD(即CD′)同时与AD交于一点F时,点E,F和点A构成△AEF。试探究△AEF的周长是否存在最小值,如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值。


解:△AEF的周长存在最小值 。理由
。理由 如下:
如下:
根据菱形和 旋转的性质,以及∠B=60°,可得△ABC,△ACD和△A′CD′是等边三角形,
旋转的性质,以及∠B=60°,可得△ABC,△ACD和△A′CD′是等边三角形,
∴∠BCA=∠BCE+∠ACE=60°,∠ECF=∠ACF+∠ACE=60° 。∴∠BCE=∠ACF。
。∴∠BCE=∠ACF。
在△BCE与△ACF中,BC=AC,∠EBC= ∠
∠ FAC
FAC =60°,∠BCE=∠ACF,
=60°,∠BCE=∠ACF,
∴△BCE≌△ACF(AS A)。∴BE=AF,CE=CF,AE+AF=AE+BE=AB。
A)。∴BE=AF,CE=CF,AE+AF=AE+BE=AB。
∵∠ECF=60°,故△ECF是等边三角形,EF=CF。
∵CF的最小值为点C到AD的距离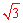 (如图
(如图 ),∴EF的最小
),∴EF的最小 值是
值是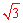 。
。
∵△AEF的周长=AE+AF+EF=AB+EF,∴△AEF的周长的最小值为2+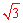 。
。
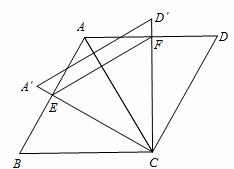
【考点】旋转的性质,菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,点到直线 距离的性质。
距离的性质。


练习册系列答案
相关题目
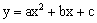 关于直线
关于直线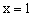 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D 在抛物线上,直线
在抛物线上,直线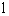 是一次函数
是一次函数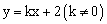 的图象,点O是坐标原点。
的图象,点O是坐标原点。 对称?若存在,求出P点坐标;若不存在,请说明理
对称?若存在,求出P点坐标;若不存在,请说明理 由.
由.
 分别与直线AB相交于点E,点F,
分别与直线AB相交于点E,点F, 当点P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2。试探究:
当点P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2。试探究: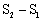 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由。
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由。
 运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<
运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<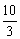
 )秒
)秒

 若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标. 中,点O为原点,点B在反比例函数
中,点O为原点,点B在反比例函数 (
( >
> )图象上,
)图象上, OB=
OB= (OC>OA).
(OC>OA). 1)
1) 时间为
时间为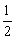 秒时,在x轴上是否
秒时,在x轴上是否 存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
 边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.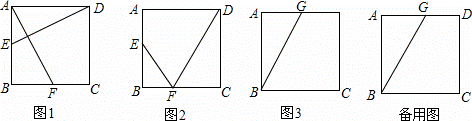


 ?若存在,求出t
?若存在,求出t 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 如图,在平面直角坐标系xOy中,A
如图,在平面直角坐标系xOy中,A (2,0),B(4,0),动点C在直线
(2,0),B(4,0),动点C在直线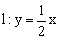 上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】