题目内容
11.一条弦把圆分成2:4两部分,则这条弦所对的圆周角的度数是60°或120°.分析 利用圆心角、弧、弦的关系得到这条弦所对的两个圆心角的比为2:4,则利用它们的和为360°可计算出这条弦所对的圆心角为120°或240°,然后根据圆周角定理可得到这条弦所对的圆周角的度数.
解答 解:∵一条弦把圆分成2:4两部分,
∴这条弦所对的两个圆心角的比为2:4,
而它们的和为360°,
∴这条弦所对的圆心角为360°×$\frac{2}{6}$=120°或360°×$\frac{4}{6}$=240°,
∴这条弦所对的圆周角的度数分别为60°或120°.
故答案为60°或120°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
1. 下面几何体的主视图是( )
下面几何体的主视图是( )
 下面几何体的主视图是( )
下面几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
16.李明靠勤工俭学的收入支付生活费,下面是李明一周的收支情况表(收入为正,支出为负,单位为元)
(1)在一周内李明有多少结余?
(2)照这样,一个月(按30天计算)李明能有多少结余?
| 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| +15 | +10 | 0 | +20 | +15 | +10 | +17 |
| -8 | -12 | -10 | -7 | -9 | -8 | -10 |
(2)照这样,一个月(按30天计算)李明能有多少结余?
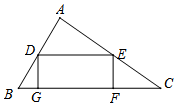 在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.
在△ABC中,BC=6,S△ABC=6,矩形DEFG内接于△ABC,其中点G、F在BC上,点D、E分别在AB、AC上,若DE:EF=k,求:四边形DEFG的面积.
 如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.
如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.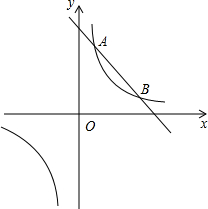 如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)
如图,反比例函数y1=$\frac{k}{x}$,(k>0)与一次函数y2=-x+5交于A(2,n)、B两点(A点在B点左边)