题目内容
3.如图,每个图形的四个数都有规律,请你根据第(1)、(2)个图形的规律,推断第(3)个图形中间的数是什么?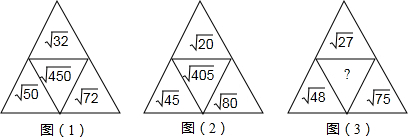
分析 由(1)知$\sqrt{32}$=4$\sqrt{2}$,$\sqrt{50}$=5$\sqrt{2}$,$\sqrt{72}$=6$\sqrt{2}$,$\sqrt{450}$=15$\sqrt{2}$,$\sqrt{32}+\sqrt{50}+\sqrt{72}=\sqrt{450}$;
由(2)知$\sqrt{20}$=2$\sqrt{5}$,$\sqrt{45}$=3$\sqrt{5}$,$\sqrt{80}$=4$\sqrt{5}$,$\sqrt{405}$=2$\sqrt{5}$$+3\sqrt{5}$$+4\sqrt{5}$=9$\sqrt{5}$,
可得:图(3)?=$\sqrt{27}$$+\sqrt{48}$$+\sqrt{75}$,可得结果.
解答 解:∵由(1)知$\sqrt{32}$=4$\sqrt{2}$,$\sqrt{50}$=5$\sqrt{2}$,$\sqrt{72}$=6$\sqrt{2}$,$\sqrt{450}$=15$\sqrt{2}$,$\sqrt{32}+\sqrt{50}+\sqrt{72}=\sqrt{450}$;
由(2)知$\sqrt{20}$=2$\sqrt{5}$,$\sqrt{45}$=3$\sqrt{5}$,$\sqrt{80}$=4$\sqrt{5}$,$\sqrt{405}$=2$\sqrt{5}$$+3\sqrt{5}$$+4\sqrt{5}$=9$\sqrt{5}$,
∴图(3)?=$\sqrt{27}$$+\sqrt{48}$$+\sqrt{75}$=3$\sqrt{3}$$+4\sqrt{3}$$+5\sqrt{3}$=12$\sqrt{3}$=$\sqrt{432}$,
故答案为:$\sqrt{432}$.
点评 本题主要考查了数字的变化规律和算术平方根,根据观察发现规律,运用规律是解答此题的关键.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案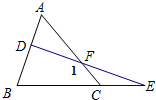 如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )
如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )| A. | ∠A+∠B=∠1+∠E | B. | ∠A+∠B=∠1-∠E | C. | ∠A-∠B=∠1-∠E | D. | ∠A-∠B=∠1+∠E |
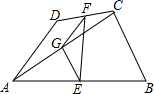 如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )| A. | 20° | B. | 24° | C. | 26° | D. | 15° |
| A. | m | B. | -m | C. | 3m | D. | -3m |
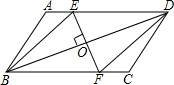 已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?
已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么? 有一艘轮船装满货物后,水面上货物宽6m,高4.4米,它能通过一座直径10m的半圆形拱桥吗?
有一艘轮船装满货物后,水面上货物宽6m,高4.4米,它能通过一座直径10m的半圆形拱桥吗? 在△ABC中,AE为角平分线,AD为中线,CF⊥AE,AB=8,AC=6,求DF的长.
在△ABC中,AE为角平分线,AD为中线,CF⊥AE,AB=8,AC=6,求DF的长.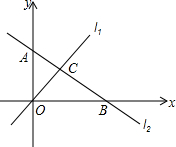 如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).
如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).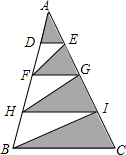 如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.
如图,三角形ABC中,将AB,AC分别四等分,已知三角形ADE的面积是6cm2,求阴影部分的面积.