题目内容
5．若方程组$\left\{\begin{array}{l}{{x}^{2}-12y=0}\\{x-3y=k}\end{array}\right.$只有一组实数解，则k的值是（ ）| A． | 1 | B． | -1 | C． | ±1 | D． | 0 |
分析 方程组有一个一次方程和一个二次方程构成，由于方程组只有一组实数解，所以一元二次方程有两个相等的实数根．把（2）代入（1），得到关于x的一元二次方程，令根的判别式为0．确定k的值．
解答 解：$\left\{\begin{array}{l}{{x}^{2}-12y=0（1）}\\{x-3y=k（2）}\end{array}\right.$由（2）得，3y=x-k（3）；把（3）代入（1）得，x2-4（x-k）=0，即x2-4x+4k=0．由于方程组只有一组实数解，所以关于x的二次方程有两个相等的实数根．△=（-4）2-4×1×4k=16-16k=0，解得k=1．
故选A．
点评 本题考查了方程组的解法和一元二次方程根的判别式．理解“只有一组实数解”，把方程组转化为一元二次方程是关键．若解决本题，变形（2）用含y的代数式表示x，题目会变的复杂．
练习册系列答案
相关题目
15．
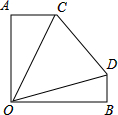如图，A在O的正北方向，B在O的正东方向，且OA=OB．某一时刻，甲车从A出发，以60km/h的速度朝正东方向行驶，与此同时，乙车从B出发，以40km/h的速度朝正北方向行驶．1小时后，位于点O处的观察员发现甲、乙两车之间的夹角为45°，即∠COD=45°，此时，甲、乙两人相距的距离为（ ）
如图，A在O的正北方向，B在O的正东方向，且OA=OB．某一时刻，甲车从A出发，以60km/h的速度朝正东方向行驶，与此同时，乙车从B出发，以40km/h的速度朝正北方向行驶．1小时后，位于点O处的观察员发现甲、乙两车之间的夹角为45°，即∠COD=45°，此时，甲、乙两人相距的距离为（ ）| A． | 90km | B． | 50$\sqrt{2}$km | C． | 20$\sqrt{13}$km | D． | 100km |
16．在平面直角坐标系中，已知点A（4，2），B（1，3），以原点O为位似中心，相似比为$\frac{1}{2}$，把△ABO缩小，则点A的对应点A′的坐标是（ ）
| A． | （2，1） | B． | （8，4） | C． | （8，4）或（-8，-4） | D． | （2，1）或（-2，-1） |
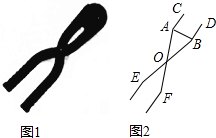双十一期间，某店铺推出的如图1的雪球夹销售火爆，其形状可近似的看成图2的图形，当雪球夹闭合时，侧得∠AOB=28°，OA=OB=14厘米，求这个雪球夹制作的雪球的直径AB的长度．（结果精确到1厘米，参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53，sin14°≈0.24，cos14°≈0.97，tan14°≈0.25．）
如图，BD为⊙O的直径，AB与⊙O相切于点B，连接AO，AO与⊙O交于点C，若∠A=30°，⊙O的半径为2，则$\widehat{CD}$的长为$\frac{4}{3}$π（结果保留π）．