题目内容
15.已知等腰三角形的周长为24,一腰上的中线把三角形分为两个三角形,两个三角形的周长的差是3cm,求等腰三角形各边的长.分析 根据题意画出图形,设等腰三角形的腰长为x,则底边长为24-2x,再根据两个三角形的周长差是3求出x的值即可.
解答 解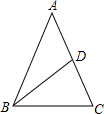 :如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=x,
:如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=x,
∵点D为AC的中点,
∴AD=CD=$\frac{1}{2}$,BC=24-(AB+AC)=24-2x.
①当△ABD的周长大于△BCD的周长时,
∵AB+AD+BD-(BC+CD+BD)=3,
∴AB-BC=3,
即x-(24-2x)=3,
解得x=9,
24-2x=6,
9,9,6能够组成三角形,符合题意;
②当△BCD的周长大于△ABD的周长时,
∵BC+CD+BD-(AB+AD+BD)=3,
∴BC-AB=3,
即24-2x-x=3,
解得x=7,
24-2x=10,
7,7,10能够组成三角形,符合题意.
综上所述,这个等腰三角形的腰长为9,底边长为6或腰长为7,底边长为10.
点评 本题考查的是等腰三角形的性质,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
5.观察下面点阵图和相应的等式,探究其中的规律:

①1=12;②1+3=22;③1+3+5=32;④1+3+5+7=42;⑤1+3+5+7+9=52;…
按此规律1+3+5+7+…+(2n-1)=( )

①1=12;②1+3=22;③1+3+5=32;④1+3+5+7=42;⑤1+3+5+7+9=52;…
按此规律1+3+5+7+…+(2n-1)=( )
| A. | 2n2 | B. | n2 | C. | (2n-1)2 | D. | (n-1)2 |
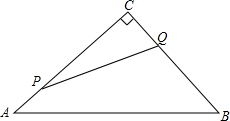 如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?
如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?