题目内容
10．多边形的对角线条数d与边数n之间的函数表达式是d=$\frac{1}{2}$n2-$\frac{3}{2}$n，d是n的二次函数．分析 可根据多边形的对角线与边的关系．n边形从一个顶点出发可引出（n-3）条对角线．从n个顶点出发引出（n-3）条，而每条重复一次，所以n边形对角线的总条数为$\frac{n（n-3）}{2}$，由此得到多边形的对角线条数d与边数n之间的函数表达式，整理得出d是n的二次函数．
解答 解：多边形的对角线条数d与边数n之间的函数表达式是d=$\frac{n（n-3）}{2}$，
整理得d=$\frac{1}{2}$n2-$\frac{3}{2}$n，
所以d是n的二次函数．
故答案为d=$\frac{1}{2}$n2-$\frac{3}{2}$n，二次．
点评 此题考查了根据实际问题列二次函数关系式，多边形的对角线，二次函数的定义，掌握好多边形对角线与边数之间的关系是解题的关键．
练习册系列答案
相关题目
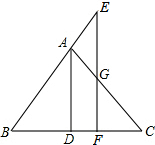如图，在△ABC中，AD⊥BC于点D，且AD平分∠BAC，点E是BA延长线上任一点，过点E作EF⊥BC于点F，与AC交于点G．
如图，在△ABC中，∠ACB=90°，CD是高，AC=4，BC=3，AB=5，求CD的长．