题目内容
5．设x1，x2是方程2x2+4x-3=0的两个根，利用根与系数的关系，求下列各式的值：（1）（x1+2）（x2+2）；
（2）$\frac{x_2}{x_1}+\frac{x_1}{x_2}$．
分析 先根据根与系数的关系得到x1+x2=-2，x1x2=-$\frac{3}{2}$，再进行代数式变形得到（1）中的原式=x1x2+2（x1+x2）+4，（2）中的原式=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{（{x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$，然后分别利用整体代入的方法计算即可．
解答 解：根据题意得x1+x2=-2，x1x2=-$\frac{3}{2}$，
（1）原式=x1x2+2（x1+x2）+4=-$\frac{3}{2}$+2×（-2）+4=-$\frac{3}{2}$；
（2）原式=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{（{x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{（-2）^{2}-2×（-\frac{3}{2}）}{-\frac{3}{2}}$=-$\frac{14}{3}$．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
请画出△PAB的三条高．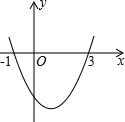
已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0）．对于下列命题：①b-2a=0；②abc＜0；③a-2b+4c＜0；④8a+c＞0．其中正确的有③④．