题目内容
5.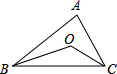 已知O为△ABC的内心,且∠BOC=130°,则∠A=80°.
已知O为△ABC的内心,且∠BOC=130°,则∠A=80°.
分析 由三角形内切圆定义可知:OB、OC是∠ABC、∠ACB的角平分线.利用内角和定理先求得∠OBC+∠OCB=50°,所以可知∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),把对应数值代入此关系式即可求得∠BAC的值.
解答 解:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=180°-130°=50°,而∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=50°,
∴∠ABC+∠ACB=100°,
∴∠BAC=180°-100°=80°.
故答案为:80°.
点评 本题考查了三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
15.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a2+2ab-b2=(a-b)2 | C. | (a3)2=a6 | D. | ab2+a2b=a3b2 |
10.边长为a的正六边形的面积等于( )
| A. | $\frac{3\sqrt{3}}{4}$a2 | B. | a2 | C. | 3$\sqrt{3}$a2 | D. | $\frac{3\sqrt{3}}{2}$a2 |
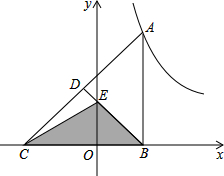 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$3\sqrt{6}$,则k的值为6$\sqrt{6}$.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$3\sqrt{6}$,则k的值为6$\sqrt{6}$.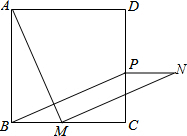 如图,在正方形ABCD中,点M是BC边上的任意一点,连接AM,并将线段AM绕点M顺时针旋转90°得到线段MN,过N作NP⊥CD于点P,连接BP.求证:四边形BMNP是平行四边形.
如图,在正方形ABCD中,点M是BC边上的任意一点,连接AM,并将线段AM绕点M顺时针旋转90°得到线段MN,过N作NP⊥CD于点P,连接BP.求证:四边形BMNP是平行四边形.
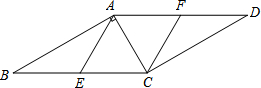 如图,已知点E,F分别是?ABCD的边BC,AD上的中点,且∠BAC=90°.
如图,已知点E,F分别是?ABCD的边BC,AD上的中点,且∠BAC=90°.