题目内容
10.边长为a的正六边形的面积等于( )| A. | $\frac{3\sqrt{3}}{4}$a2 | B. | a2 | C. | 3$\sqrt{3}$a2 | D. | $\frac{3\sqrt{3}}{2}$a2 |
分析 边长为a的正六边形的面积是边长是a的等边三角形的面积的6倍,据此即可求解.
解答 解:边长为a的等边三角形的面积是:$\frac{\sqrt{3}}{4}$a2,
则边长为a的正六边形的面积等于6×$\frac{\sqrt{3}}{4}$a2=$\frac{3\sqrt{3}}{2}$a2.
故选D.
点评 本题考查的是正多边形和圆,熟知正多边形的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.-2是2的( )
| A. | 倒数 | B. | 绝对值 | C. | 平方根 | D. | 相反数 |
2.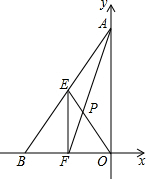 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P的坐标为( )| A. | (-1,$\frac{4}{3}$) | B. | (-$\frac{3}{2}$,2) | C. | (-$\frac{3}{2}$,$\frac{4}{3}$) | D. | (-1,2) |
19.某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )
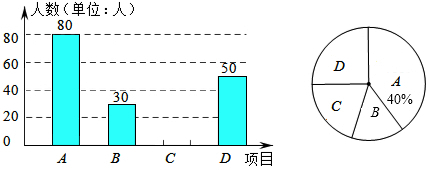

| A. | 240 | B. | 120 | C. | 80 | D. | 40 |
20.方程2x-1=3x+2的解为( )
| A. | x=1 | B. | x=-1 | C. | x=3 | D. | x=-3 |
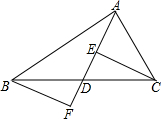 如图:在△ABC中,点D为BC边上的中点,连接AD,点E为线段AD上的一点,连接CE,过点B作BF∥CE交AD的延长线于点F,求证:CE=BF.
如图:在△ABC中,点D为BC边上的中点,连接AD,点E为线段AD上的一点,连接CE,过点B作BF∥CE交AD的延长线于点F,求证:CE=BF.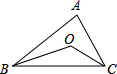 已知O为△ABC的内心,且∠BOC=130°,则∠A=80°.
已知O为△ABC的内心,且∠BOC=130°,则∠A=80°.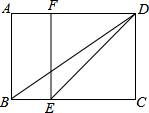 已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.
已知:如图,在矩形ABCD中,E是BC边上一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.