题目内容
19.已知二次函数y=(x-h)2+1(h为常数),在自变量x满足2≤x≤4的情况下,y的最小值为10,则h的值为-1或7.分析 由解析式可知该函数在x=h时取得最小值10、x>h时,y随x的增大而增大、当x<h时,y随x的增大而减小,根据2≤x≤4时,函数的最小值为10可分如下两种情况:①若h<2≤x≤4,x=2时,y取得最小值10;②若2≤x≤4<h,当x=4时,y取得最小值10,分别列出关于h的方程求解即可.
解答 解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,
∴①若h<2≤x≤4,x=2时,y取得最小值10,
可得:(2-h)2+1=10,
解得:h=-1或h=5(舍去);
②若2≤x≤4<h,当x=4时,y取得最小值10,
可得:(4-h)2+1=10,
解得:h=7或h=1(舍去).
综上,h的值为-1或7,
故答案为:-1或7.
点评 本题主要考查二次函数的性质和最值,根据二次函数的性质和最值分类讨论是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
7. 小李在平面直角坐标系中画了一张示意图,分别标出了学校、电影院、体育馆、超市的大致位置,如果张大妈从体育馆向南走150米,再向东走400米,再向南走250米,再向西走50米,最终到达的地点是( )
小李在平面直角坐标系中画了一张示意图,分别标出了学校、电影院、体育馆、超市的大致位置,如果张大妈从体育馆向南走150米,再向东走400米,再向南走250米,再向西走50米,最终到达的地点是( )
 小李在平面直角坐标系中画了一张示意图,分别标出了学校、电影院、体育馆、超市的大致位置,如果张大妈从体育馆向南走150米,再向东走400米,再向南走250米,再向西走50米,最终到达的地点是( )
小李在平面直角坐标系中画了一张示意图,分别标出了学校、电影院、体育馆、超市的大致位置,如果张大妈从体育馆向南走150米,再向东走400米,再向南走250米,再向西走50米,最终到达的地点是( )| A. | 学校 | B. | 电影院 | C. | 体育馆 | D. | 超市 |
14.下列方程中,没有实数根的是( )
| A. | 2x2-5x-4=0 | B. | 7t2-5t+2=0 | C. | x(x+1)=3 | D. | 3y2+25=10$\sqrt{3}$y |
8. 如图所示,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点D是AB的中点,连接C、D两点,则CD=( )
如图所示,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点D是AB的中点,连接C、D两点,则CD=( )
 如图所示,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点D是AB的中点,连接C、D两点,则CD=( )
如图所示,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点D是AB的中点,连接C、D两点,则CD=( )| A. | 2.5 | B. | 3 | C. | 5 | D. | 2.4 |
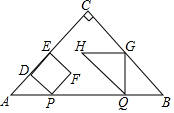 如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC-CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).
如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC-CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4). 直线y=kx+b如图,则关于x的不等式kx+b≤-2的解集是x≥-1.
直线y=kx+b如图,则关于x的不等式kx+b≤-2的解集是x≥-1.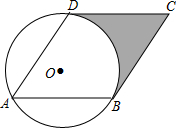 已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.