题目内容
 在“母亲节”期间,某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价(整数)x(元/个)之间的对应关系如图所示:
在“母亲节”期间,某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价(整数)x(元/个)之间的对应关系如图所示:(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若购进一批许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润;
(3)若销售许愿瓶所得利润不低于1350元,试结合函数图象,确定这种许愿瓶的销售单价的范围.
考点:二次函数的应用
专题:
分析:(1)根据图象可以得出设y与x之间的函数关系为y=kx+b,直接运用待定系数法求出其解就可以了;
(2)根据条件建立不等式求出x的取值范围,再根据利润等于售价-进价表示出总利润,由二次函数的性质就可以求出结论;
(3)先根据条件建立一元二次不等式,求出一元二次不等式的解即可求出销售单价的范围.
(2)根据条件建立不等式求出x的取值范围,再根据利润等于售价-进价表示出总利润,由二次函数的性质就可以求出结论;
(3)先根据条件建立一元二次不等式,求出一元二次不等式的解即可求出销售单价的范围.
解答:解:(1)设y与x之间的函数关系为y=kx+b,由题意,得
,
解得:
,
故y与x之间的函数关系式为:y=-30x+600;
(2)由题意,得
6(-30x+600)≤900,
解得:x≥15,
设销售这种许愿瓶的利润为W元,由题意,得
W=(x-6)(-30x+600),
=-30x2+780x-3600,
∴图象对称轴为x=-
=13,
∵a=-30<0,
∴抛物线开口向下,当x≥15时,w随x增大而减小,
∴当x=15时,w最大=1350.
(3)由题意,得
-30x2+780x-3600≥1350,
x2-26x+165≤0,
∴(x-11)(x-15)≤0
∴①
或②
,
解①得,原不等式组无解,
解②得,原不等式组的解集为:11≤x≤15,
∴这种许愿瓶的销售单价的范围为:11≤x≤15.
|
解得:
|
故y与x之间的函数关系式为:y=-30x+600;
(2)由题意,得
6(-30x+600)≤900,
解得:x≥15,
设销售这种许愿瓶的利润为W元,由题意,得
W=(x-6)(-30x+600),
=-30x2+780x-3600,
∴图象对称轴为x=-
| 780 |
| 2×(-30) |
∵a=-30<0,
∴抛物线开口向下,当x≥15时,w随x增大而减小,
∴当x=15时,w最大=1350.
(3)由题意,得
-30x2+780x-3600≥1350,
x2-26x+165≤0,
∴(x-11)(x-15)≤0
∴①
|
|
解①得,原不等式组无解,
解②得,原不等式组的解集为:11≤x≤15,
∴这种许愿瓶的销售单价的范围为:11≤x≤15.
点评:本题是一道二次函数的综合运用试题,考查了待定系数法求一次函数的解析式的运用,二次函数的性质的运用,一元二次不等式的解法的运用,解答时求出利润的解析式是关键.

练习册系列答案
相关题目
 如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=
如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=| k |
| x |
| A、S是变化的,因为菱形CDEF中只有C点的位置是确定的,其它三点都不是固定的 | ||||||||||
| B、当D点从C点到B点运动时,S逐渐增大 | ||||||||||
| C、从图上看,可以用两个菱形的面积减去两个三角形的面积,但E、F两点不确定,所以还是不能求出 | ||||||||||
D、如果连接CE,则CE∥OB,△OBE与△OBC同底(OB)共高,则S△OBE=S△OBC,OC=OA=2
|
下列调查方式合适的是( )
| A、为了了解九年级学生数学作业的时间,校长对九年级一班的3位同学进行了抽样调查 |
| B、为了了解全国青少年的睡眠时间,调研人员对某市七年级学生进行了调查 |
| C、为了了解重庆人民对建设“五个重庆”的感受,记者到某中学随机采访了20名老师 |
| D、为了了解我国新引进的一架飞机的安全性能,检查人员采用了普查的方式 |
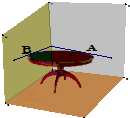 小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )| A、45° |
| B、135° |
| C、45°或135° |
| D、90°或135° |

 如图,抛物线y=x2,y=
如图,抛物线y=x2,y= 某批发商6月1日以70元/千克的成本价购入了某海产品1 000千克,据市场预测,该产品的销售价y(元/千克)与时间x(天)之间函数关系的图象如图中的折线段ABC所示.
某批发商6月1日以70元/千克的成本价购入了某海产品1 000千克,据市场预测,该产品的销售价y(元/千克)与时间x(天)之间函数关系的图象如图中的折线段ABC所示.