题目内容
 如图,抛物线y=x2,y=
如图,抛物线y=x2,y=| 1 |
| 2 |
| 1 |
| 4 |
考点:二次函数的性质
专题:
分析:把点A的横坐标代入函数解析式求出点A、B的纵坐标,从而求出AB的长度,再根据二次函数的对称性求出BC的长,并得到阴影部分的面积等于矩形ABCD的面积的一半,然后列式计算即可得解.
解答:解:∵点A的横坐标为-1,
∴y=
×(-1)2=
,
y=-
×(-1)2=-
,
∴点A(-1,
),B(-1,-
),
∴AB=
-(-
)=
,
根据二次函数的对称性,BC=1×2=2,
阴影部分的面积=
S矩形ABCD=
×2×
=
.
故答案为:
.
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
y=-
| 1 |
| 4 |
| 1 |
| 4 |
∴点A(-1,
| 1 |
| 2 |
| 1 |
| 4 |
∴AB=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
根据二次函数的对称性,BC=1×2=2,
阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查了二次函数的性质,主要利用了二次函数图象上点的坐标特征,二次函数的对称性,判断出阴影部分的面积等于矩形的面积的一半是解题的关键,也是本题的难点.

练习册系列答案
相关题目
观察下列图形,第1个图形中有4个三角形,第二个图形中有12个三角形,…,则第10个图形中三角形的个数是( )


| A、4000 | B、92 |
| C、76 | D、84 |
若x=-2是关于x的方程2x+3m+1=0的解,则m的值为( )
A、
| ||
B、-
| ||
| C、-1 | ||
| D、1 |
 已知:如图,AB=2,点C在BD上,BC=1,BD=4,AC=2.4.
已知:如图,AB=2,点C在BD上,BC=1,BD=4,AC=2.4.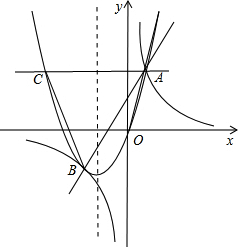 如图,抛物线y=ax2+bx(a>0)与双曲线
如图,抛物线y=ax2+bx(a>0)与双曲线 已知集合A中的数与集合B中对应的数之间的关系是某个二次函数.若用x表示集合A中的数,用y表示集合B中的数,由于粗心,小颖算错了集合B中的一个y值,请你指出这个算错的y值为
已知集合A中的数与集合B中对应的数之间的关系是某个二次函数.若用x表示集合A中的数,用y表示集合B中的数,由于粗心,小颖算错了集合B中的一个y值,请你指出这个算错的y值为 在“母亲节”期间,某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价(整数)x(元/个)之间的对应关系如图所示:
在“母亲节”期间,某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价(整数)x(元/个)之间的对应关系如图所示: 如图,方格纸中有一条美丽可爱的小金鱼.
如图,方格纸中有一条美丽可爱的小金鱼.