题目内容
13.在平面直角坐标系xOy中,抛物线y=mx2-4mx(m≠0)与x轴交于A,B两点(点A在点B的左侧).(1)求点A,B的坐标及抛物线的对称轴;
(2)过点B的直线l与y轴交于点C,且tan∠ACB=2,直接写出直线l的表达式;
(3)如果点P(x1,n)和点Q(x2,n)在函数y=mx2-4mx(m≠0)的图象上,PQ=2a且x1>x2,求x12+ax2-6a+2的值.
分析 (1)利用二次函数图象上点的坐标特征即可求出点A、B的坐标,再根据二次函数的性质即可求出抛物线的对称轴;
(2)分点C在y轴正半轴以及负半轴考虑,由tan∠ACB的值可得出点C的坐标,根据点B、C的坐标利用待定系数法,即可求出直线l的表达式;
(3)由点P、Q的纵坐标相同,可得出点P与点Q关于对称轴x=2对称,根据PQ=2a且x1>x2,即可得出x1=2+a、x2=2-a,将其代入x12+ax2-6a+2中,即可得出结论.
解答 解:(1)当y=mx2-4mx=mx(x-4)=0时,x1=0,x2=4,
∵点A在点B的左侧,
∴A点坐标为(0,0),B点坐标为(4,0).
抛物线对称轴为直线:x=-$\frac{-4m}{2m}$=2.
(2)设直线l的表达式为y=kx+b(k≠0).
当点C在y轴正半轴时,点C的坐标为(0,2),
将B(4,0)、C(0,2)代入y=kx+b中,
$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
此时直线l的表达式为y=-$\frac{1}{2}$x+2;
当点C在y轴负半轴时,点C的坐标为(0,-2),
将B(4,0)、C(0,-2)代入y=kx+b中,
$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$,
此时直线l的表达式为y=$\frac{1}{2}$x-2.
综上所述:直线l的表达式为y=-$\frac{1}{2}$x+2或y=$\frac{1}{2}$x-2.
(3)∵点P(x1,n)和点Q(x2,n)在函数y=mx2-4mx(m≠0)的图象上,
∴点P与点Q关于对称轴x=2对称.
∵PQ=2a,x1>x2,
∴x1=2+a,x2=2-a,
∴x12+ax2-6a+2=(2+a)2+a(2-a)-6a+2=6.
点评 本题考查了抛物线与x轴的交点、解直角三角形、二次函数的性质、二次函数图象上点的坐标特征以及待定系数法求一次函数解析式,解题的关键是:(1)利用二次函数图象上点的坐标特征求出点A、B的坐标;(2)根据点B、C的坐标,利用待定系数法求出直线l的表达式;(3)由点P、Q坐标的特征结合PQ=2a,找出x1=2+a、x2=2-a.

 口算题天天练系列答案
口算题天天练系列答案| A. | 这组数据的众数是170 | |
| B. | 这组数据的中位数是169 | |
| C. | 这组数据的平均数是169 | |
| D. | 若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为$\frac{1}{2}$ |
 如图所示,在△ABC中,AB=AC,∠A=36°.
如图所示,在△ABC中,AB=AC,∠A=36°. 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面相对面上的字是中.
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面相对面上的字是中.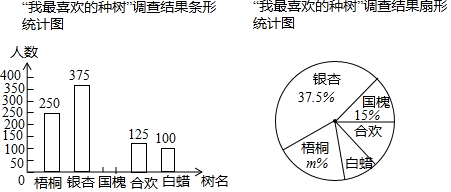
 春季,某校开展植树活动,甲、乙两班接到了植树任务,甲班先植树一段时间后乙班参加了植树活动,两班一起植树一段时间后,甲班临时承担了浇水任务,剩下的任务由乙班单独完成,乙班提高了工作效率,每小时比原来多植树15棵,结果按时完成了任务.设两班植树的总数量为y(棵),两班一起植树的时间(从甲班开始植树时计时)为x(时),y与x之间的函数图象如图所示.
春季,某校开展植树活动,甲、乙两班接到了植树任务,甲班先植树一段时间后乙班参加了植树活动,两班一起植树一段时间后,甲班临时承担了浇水任务,剩下的任务由乙班单独完成,乙班提高了工作效率,每小时比原来多植树15棵,结果按时完成了任务.设两班植树的总数量为y(棵),两班一起植树的时间(从甲班开始植树时计时)为x(时),y与x之间的函数图象如图所示. 如图所示的几何体是由五个相同的小正方体组合而成的,则它的左视图是( )
如图所示的几何体是由五个相同的小正方体组合而成的,则它的左视图是( )



 (1)计算:|-2|-3tan30°+(2-$\sqrt{3}$)0+$\sqrt{12}$
(1)计算:|-2|-3tan30°+(2-$\sqrt{3}$)0+$\sqrt{12}$