题目内容
17.甲、乙二人解方程组$\left\{\begin{array}{l}{mx+y=-3,①}\\{2x-ny=-3,②}\end{array}\right.$,由于甲看错了方程②中的n的值,得到方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,而乙看错了方程①中的m的值,得到方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$,请问原方程组的正确的解为多少?分析 把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入方程组第一个方程求出m的值,把$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$代入第二个方程求出n的值,确定出原方程组,再求解即可.
解答 解:把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入①得:-m-2=-3,即m=1;
把$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入②得:-2+2n=-3,即n=-$\frac{1}{2}$,
故方程组为$\left\{\begin{array}{l}{x+y=-3①}\\{2x+\frac{1}{2}y=-3②}\end{array}\right.$,
②×2-①得:3x=-3,即x=-1,
把x=-1代入①得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$.
点评 本题考查的是二元一次方程的解,解答此题关键是将每一个解代入没有看错的方程中,分别求m、n的值.

练习册系列答案
相关题目
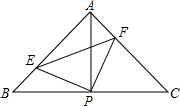 如图,已知△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: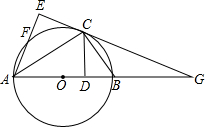 如图,在Rt△AEG中,∠E=90°,∠EAG的平分数交EG于C,过C作AC的垂线交AG于B,以AB为直径的⊙O交AE于F
如图,在Rt△AEG中,∠E=90°,∠EAG的平分数交EG于C,过C作AC的垂线交AG于B,以AB为直径的⊙O交AE于F 如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.
如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.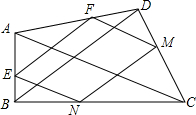 如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.
如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.