题目内容
4.已知函数y=-$\frac{1}{2}$(x+3)2-2,回答下列问题:(1)写出函数图象的开口方向,对称轴和顶点坐标.
(2)当x在什么范围内,函数值y随x的增大而减小?
分析 (1)根据二次函数的图象与系数的关系及顶点式即可得出结论;
(2)根据二次函数的开口方向及对称轴方程即可得出结论.
解答 解:(1)∵a=-$\frac{1}{2}$<0,
∴函数图象的开口向下;
∵函数的解析式为:y=-$\frac{1}{2}$(x+3)2-2,
∴对称轴为直线x=-3,顶点坐标为(-3,-2);
(2)∵函数图象的开口向下,对称轴为直线x=-3,
∴当x>-3时,函数值y随x的增大而减小.
点评 本题考查的是二次函数的性质,熟知二次函数的顶点式及函数的图象与系数的关系是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
16.3$\frac{2}{7}$与(-2$\frac{5}{7}}$)的和是( )
| A. | $-\frac{3}{7}$ | B. | $1\frac{1}{7}$ | C. | $-\frac{3}{7}$ | D. | $\frac{4}{7}$ |
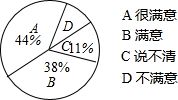 某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.
某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名. 某洗发水的原价如图所示,则现价为45元.
某洗发水的原价如图所示,则现价为45元.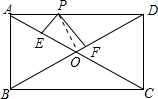 如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长.
如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长. 如图,阴影部分的面积为51.
如图,阴影部分的面积为51. 如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.