题目内容
 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.(1)如果∠AOB=150°,那么∠COE是多少度;
(2)在(1)的条件下,如果∠COD=30°,那么∠BOE是多少度?
考点:角平分线的定义
专题:
分析:(1)先根据OC是∠AOD的平分线,OE是∠BOD的平分线得出∠COD=
∠AOD,∠DOE=
∠BOD,再由∠COE=∠COD+∠DOE即可得出结论;
(2)根据(1)可知∠COE的度数,由∠COD=30°可得出∠DOE的度数,由角平分线的定义即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据(1)可知∠COE的度数,由∠COD=30°可得出∠DOE的度数,由角平分线的定义即可得出结论.
解答:解:(1)∵OC是∠AOD的平分线,OE是∠BOD的平分线,
∴∠COD=
∠AOD,∠DOE=
∠BOD,
∴∠COE=∠COD+∠DOE=
(∠AOD+∠BOD)=
∠AOB=
×150°=75°;
(2)∵∠COD=30°,由(1)知,∠COE=75°,
∴∠DOE=75°-30°=45°.
∵OE是∠BOD的平分线,
∴∠BOE=∠DOE=45°.
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COE=∠COD+∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵∠COD=30°,由(1)知,∠COE=75°,
∴∠DOE=75°-30°=45°.
∵OE是∠BOD的平分线,
∴∠BOE=∠DOE=45°.
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知⊙A的半径为2,AB的距离是3,则点B在⊙A( )
| A、点B在⊙A内 |
| B、点B在⊙A上 |
| C、点B在⊙A外 |
| D、不确定 |
 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠A=30°,DE=1,则DF的长是
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠A=30°,DE=1,则DF的长是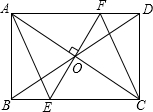 如图,O为矩形ABCD对角线的交点,过O作EF⊥AC,分别交AD、BC于F、E,若AB=2cm,BC=4cm.
如图,O为矩形ABCD对角线的交点,过O作EF⊥AC,分别交AD、BC于F、E,若AB=2cm,BC=4cm.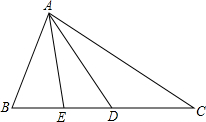 如图:在△ABC中,D是BC上一点,E是BD的中点,并且AB=DC,AE=
如图:在△ABC中,D是BC上一点,E是BD的中点,并且AB=DC,AE= 在坐标系中画出直线y=-
在坐标系中画出直线y=-