题目内容
 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠A=30°,DE=1,则DF的长是
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠A=30°,DE=1,则DF的长是考点:全等三角形的判定与性质,勾股定理
专题:
分析:易证BC=BD,即可证明△ACB≌△FDB,可得DF=AC,BD=BC,易证∠EBA=∠A=30°,即可求得BC的长,即可求得AC的长,即可解题.
解答:解:∵在Rt△ABC中,∠ACB=90°,∠A=30°,
∴AB=2BC,
∵AB=2BD,
∴BC=BD,
∵在△ACB和△FDB中,
,
∴△ACB≌△FDB,(ASA)
∴DF=AC,BD=BC,
∵DE垂直平分AB,
∴BE=AE,
∴∠EBA=∠A=30°,
∴BE=2DE=2,∴BC=
,
∴DF=AC=
BC=3,
故答案为 3.
∴AB=2BC,
∵AB=2BD,
∴BC=BD,
∵在△ACB和△FDB中,
|
∴△ACB≌△FDB,(ASA)
∴DF=AC,BD=BC,
∵DE垂直平分AB,
∴BE=AE,
∴∠EBA=∠A=30°,
∴BE=2DE=2,∴BC=
| 3 |
∴DF=AC=
| 3 |
故答案为 3.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了垂直平分线的性质,本题中求证△ACB≌△FDB是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
下列方程是一元二次方程的是( )
| A、x2+2y-3=0 | ||||||
| B、y2=0 | ||||||
| C、x(x-5)=y2-2y | ||||||
D、
|
已知函数y=2x+b的图象经过点(a,10)和(-2,a),则b值为( )
| A、6 | B、2 | C、-2 | D、-6 |
下列计算正确的是( )
A、2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
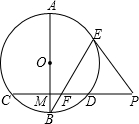 如图,AB是⊙O的直径,弦CD⊥AB于M,P是CD延长线上一点,PE切⊙O于E,BE交CD于F.求证:PF2=PD•PC.
如图,AB是⊙O的直径,弦CD⊥AB于M,P是CD延长线上一点,PE切⊙O于E,BE交CD于F.求证:PF2=PD•PC. 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.