题目内容
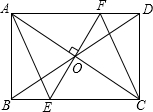 如图,O为矩形ABCD对角线的交点,过O作EF⊥AC,分别交AD、BC于F、E,若AB=2cm,BC=4cm.
如图,O为矩形ABCD对角线的交点,过O作EF⊥AC,分别交AD、BC于F、E,若AB=2cm,BC=4cm.(1)求四边形AECF的面积;
(2)求EF的长.
考点:菱形的判定与性质,矩形的性质
专题:
分析:(1)易证∠OAD=∠OCB,即可证明△AOF≌△COE,可得EO=FO,即可判定四边形AECF为菱形,AE=CE,根据在RT△ABE中,满足AB2+BE2=AE2,即可求得CE的长,即可解题;
(2)根据勾股定理可求得AC的长,再根据菱形面积计算公式即可求得EF的长,即可解题.
(2)根据勾股定理可求得AC的长,再根据菱形面积计算公式即可求得EF的长,即可解题.
解答:解:(1)∵AF∥BC,
∴∠OAD=∠OCB,
∵O为矩形ABCD对角线的交点,
∴OA=OC,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴EO=FO,
∵AO=CO,
∴四边形AECF为菱形,
∴AE=CE,
设BE=x,则AE=CE=4-x,
在RT△ABE中,22+x2=(4-x)2,
解得:x=
cm,
∴CE=
cm,
∴四边形AECF的面积=CE•AB=5cm2;
(2)∵四边形AECF的面积=5cm2=
AC•EF,
∴EF=
,
∵在RT△ABC中,AC2=AB2+BC2,
∴AC=2
cm,
∴EF=
=
cm.
∴∠OAD=∠OCB,
∵O为矩形ABCD对角线的交点,
∴OA=OC,
在△AOF和△COE中,
|
∴△AOF≌△COE(ASA),
∴EO=FO,
∵AO=CO,
∴四边形AECF为菱形,
∴AE=CE,
设BE=x,则AE=CE=4-x,
在RT△ABE中,22+x2=(4-x)2,
解得:x=
| 3 |
| 2 |
∴CE=
| 5 |
| 2 |
∴四边形AECF的面积=CE•AB=5cm2;
(2)∵四边形AECF的面积=5cm2=
| 1 |
| 2 |
∴EF=
| 10 |
| AC |
∵在RT△ABC中,AC2=AB2+BC2,
∴AC=2
| 5 |
∴EF=
| 10 |
| AC |
| 5 |
点评:本题考查了菱形的判定和菱形各边长相等的性质,考查了菱形的面积计算公式,本题中判定四边形AECF为菱形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
A、2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
反比例函数y=
,当x<0时,y随x的增大而增大,则( )
| 2m+1 |
| x |
A、m>-
| ||
B、m<-
| ||
C、m=-
| ||
| D、m只能为0 |
 如图,由四个小立方体组成的几何体中,若每个小立方体的棱长都为1,则该几何体从正面看得到的平面图形面积是
如图,由四个小立方体组成的几何体中,若每个小立方体的棱长都为1,则该几何体从正面看得到的平面图形面积是 在一条大的河流中有一形如三角形的小岛,如图,岸与小岛有一桥相连,现准备在小岛的三边上各设立一个水质取样点,水利部门在岸边设立了一个观察站,每天有专人从观察站步行去三个取样点取样,然后带去化验,请问:三个取样点应分别设在什么位置,才能使每天取样所用的时间最短?(假设行走速度不变)
在一条大的河流中有一形如三角形的小岛,如图,岸与小岛有一桥相连,现准备在小岛的三边上各设立一个水质取样点,水利部门在岸边设立了一个观察站,每天有专人从观察站步行去三个取样点取样,然后带去化验,请问:三个取样点应分别设在什么位置,才能使每天取样所用的时间最短?(假设行走速度不变) 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.