题目内容

4．已知tanA=2，求$\frac{2sinA-cosA}{4sinA+5cosA}$的值．

分析 根据同角三角函数的关系tanA=$\frac{sinA}{cosA}$=2，则sinA=2cosA，然后把sinA=2cosA代入$\frac{2sinA-cosA}{4sinA+5cosA}$中进行分式的运算即可．

解答 解：∵tanA=$\frac{sinA}{cosA}$=2，
∴sinA=2cosA，
∴$\frac{2sinA-cosA}{4sinA+5cosA}$=$\frac{4cosA-cosA}{8cosA+5cosA}$=$\frac{3}{13}$．

点评 本题考查了同角三角函数的关系：平方关系：sin2A+cos2A=1；正余弦与正切之间的关系（积的关系）：一个角的正切值等于这个角的正弦与余弦的比，即tanA=$\frac{sinA}{cosA}$或sinA=tanA•cosA．

练习册系列答案
相关题目
14．根据下面给出的条件，解答下面的问题：（填空）
（1）如果A表示的数是5，B表示的数是1，那么到A，B距离相等的点表示的数是3；
（2）如果A表示的数是3，B表示的数是-1，那么到A，B距离相等的点表示的数是1；
（3）如果A表示的数是a，B表示的数是b，那么到A，B距离相等的点表示的数是$\frac{1}{2}$（a+b）；
（4）如果A表示的数是a，B表示的数比a的相反数大2，那么到A，B距离相等的点表示的数是1．
15．计算$\frac{b}{a}$•$\frac{{a}^{2}-a}{b}$的结果是（　　）
A．a+1B．a-1C．ab-1D．ab-b
12．已知关于x的方程（m+3）x|m|-2+6m=0…①与nx-5=x（3-n）…②的解相同，其中方程①是一元一次方程，求代数式（m+x+1）2016•（-m2n+xn2）+1的值．
19．计算：
（1）$\sqrt{18}$-$\frac{3}{\sqrt{2}}$+2$\sqrt{2}$
（2）$\frac{\sqrt{28}-\sqrt{14}}{\sqrt{7}}$．
9．若$\frac{x}{y}$=$\frac{m}{n}$=$\frac{4}{5}$（y≠n），则$\frac{x-m}{y-n}$=$\frac{4}{5}$．
16．先化简，再求值：$\frac{x-1}{{x}^{2}-4x+4}•\frac{{x}^{2}-4}{{x}^{2}-1}÷\frac{x+2}{{x}^{2}+2x+1}$，其中x=3．
13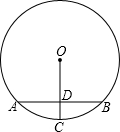．如图，O是圆心，半径OC⊥弦AB于点D，AB=8，OD=3，则CD等于（　　）
A．2B．3C．2$\sqrt{2}$D．2$\sqrt{3}$
15．$\frac{2}{3}$的倒数是$\frac{3}{2}$；-3.5的相反数为3.5；绝对值是3的数是±3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网