题目内容
 如图,正方形DECF内接于Rt△ABC中,D在斜边AB上,且AD=4cm,BD=3cm,则图中阴影部分的面积为_____cm2.
如图,正方形DECF内接于Rt△ABC中,D在斜边AB上,且AD=4cm,BD=3cm,则图中阴影部分的面积为_____cm2.
- A.5
- B.6
- C.7
- D.8
B
分析:设正方形的边长为a,由ED∥BC,DF∥AC,得到ED:BC=AD:AB,DF:AC=DB:AB,可求得BC=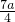 ,AC=
,AC=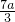 ,在Rt△ABC中,利用勾股定理得到a=
,在Rt△ABC中,利用勾股定理得到a= ,于是得到BC=
,于是得到BC=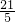 ,AC=
,AC=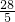 ,而S阴影部分=S△ACB-S正方形ECFD,运用三角形和正方形的面积公式即可得到答案.
,而S阴影部分=S△ACB-S正方形ECFD,运用三角形和正方形的面积公式即可得到答案.
解答: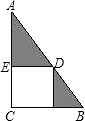 解:设正方形的边长为a,
解:设正方形的边长为a,
∵正方形DECF内接于Rt△ABC中,即ED∥BC,DF∥AC,
∴△AED∽△ACB,△BDF∽△BAC,
∴ED:BC=AD:AB,DF:AC=DB:AB,
而AD=4,BD=3,
∴BC=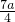 ,AC=
,AC=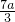 ,
,
又∵AB2=BC2+AC2,
∴(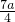 )2+(
)2+(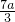 )2=72,
)2=72,
解得,a= ,
,
∴BC=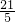 ,AC=
,AC=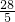 ,
,
∴S阴影部分=S△ACB-S正方形ECFD= ×
×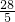 ×
×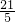 -(
-( )2=6(cm2).
)2=6(cm2).
故选B.
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线与三角形其它两边相角,所截得的三角形与原三角形相似.也考查了正方形的性质和勾股定理.
分析:设正方形的边长为a,由ED∥BC,DF∥AC,得到ED:BC=AD:AB,DF:AC=DB:AB,可求得BC=
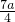 ,AC=
,AC=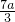 ,在Rt△ABC中,利用勾股定理得到a=
,在Rt△ABC中,利用勾股定理得到a= ,于是得到BC=
,于是得到BC=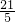 ,AC=
,AC=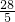 ,而S阴影部分=S△ACB-S正方形ECFD,运用三角形和正方形的面积公式即可得到答案.
,而S阴影部分=S△ACB-S正方形ECFD,运用三角形和正方形的面积公式即可得到答案.解答:
 解:设正方形的边长为a,
解:设正方形的边长为a,∵正方形DECF内接于Rt△ABC中,即ED∥BC,DF∥AC,
∴△AED∽△ACB,△BDF∽△BAC,
∴ED:BC=AD:AB,DF:AC=DB:AB,
而AD=4,BD=3,
∴BC=
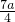 ,AC=
,AC=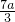 ,
,又∵AB2=BC2+AC2,
∴(
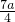 )2+(
)2+(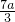 )2=72,
)2=72,解得,a=
 ,
,∴BC=
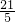 ,AC=
,AC=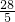 ,
,∴S阴影部分=S△ACB-S正方形ECFD=
 ×
×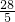 ×
×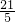 -(
-( )2=6(cm2).
)2=6(cm2).故选B.
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线与三角形其它两边相角,所截得的三角形与原三角形相似.也考查了正方形的性质和勾股定理.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
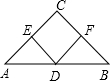 如图Rt△ABC中,D斜边AB的中点,过D分别作DE⊥AC,DF⊥BC,垂足为E,F,则四边形DECF是正方形还需添加的条件是
如图Rt△ABC中,D斜边AB的中点,过D分别作DE⊥AC,DF⊥BC,垂足为E,F,则四边形DECF是正方形还需添加的条件是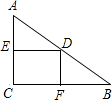 如图,在Rt△ABC中,∠C=90°,DE垂直平分AC,DF⊥BC,当△ABC满足条件
如图,在Rt△ABC中,∠C=90°,DE垂直平分AC,DF⊥BC,当△ABC满足条件 如图,在Rt△ABC中,∠ACB=90°,D在AB上,四边形DECF是正方形,若BD=3cm,AD=2cm,则图中阴影部分面积为
如图,在Rt△ABC中,∠ACB=90°,D在AB上,四边形DECF是正方形,若BD=3cm,AD=2cm,则图中阴影部分面积为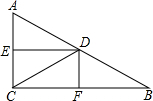 如图,Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,连接DE、DF、CD,如果
如图,Rt△ABC中,∠ACB=90°,D、E、F分别是AB、AC、BC的中点,连接DE、DF、CD,如果