Question

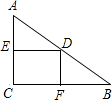如图，在Rt△ABC中，∠C=90°，DE垂直平分AC，DF⊥BC，当△ABC满足条件

 

时，四边形DECF是正方形． 
（要求：①不再添加任何辅助线，②只需填一个符合要求的条件）

Answer 1

分析：由已知可得四边形的四个角都为直角，因此再有四边相等即是正方形添加条件．此题可从四边形DECF是正方形推出．

解答：解：设AC=BC，即△ABC为等腰直角三角形，
∵∠C=90°，DE垂直平分AC，DF⊥BC，
∴∠C=∠CED=∠EDF=∠DFC=90°，
DF=

1

2

AC=CE，
DE=

1

2

BC=CF，
∴DF=CE=DE=CF，
∴四边形DECF是正方形，
故答案为：AC=BC．

点评：此题考查的知识点是正方形的判定，解题的关键是可从四边形DECF是正方形推出△ABC满足的条件．