Question

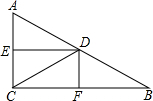如图，Rt△ABC中，∠ACB=90°，D、E、F分别是AB、AC、BC的中点，连接DE、DF、CD，如果

AC=CB

，那么四边形DECF是正方形（要求：①不再添加辅助线；
②只需填出一个符合要求的条件）．

Answer 1

分析：本题可根据正方形的判定方法填空，由已知条件可首先能判定四边形DECF为矩形，根据邻边相等的矩形为正方形可知AC=BC时结论即可成立．

解答：解：AC=BC．
证明：∵D、E、F分别是AB、AC、BC的中点，
∴DE∥BC，DE=

1

2

BC，
∵∠ACB=90°，
∴∠DEC=90°，
同理∠DFC=90°，DF=

1

2

AC，
∴四边形DECF是矩形，
又∵AC=BC，
∴DE=DF，
∴四边形DECF为正方形．
故答案为：AC=BC．（此题答案不唯一）

点评：本题考查了三角形的中位线定理、矩形的判定方法和正方形的判定方法．