题目内容
7.若关于x的一元二次方程nx2-2(n-1)x+n-2=0有两个正整数根,则整数n=-1或-2.分析 将方程左边因式分解可得方程的两根为x=1或x=1-$\frac{2}{n}$,根据x为正整数且n为整数可得n的值.
解答 解:方程左边因式分解得:[nx-(n-2)](x-1)=0,
∴nx=n-2或x=1,
∵n≠0,
∴x=$\frac{n-2}{n}$=1-$\frac{2}{n}$,
又∵x为正整数,
∴n=-1时,x=3;n=-2时,x=2;
即整数n=-1或-2,
故答案为:-1或-2.
点评 本题主要考查一元二次方程的根的情况,通过因式分解表示出方程的根是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17.下列运算正确的是( )
| A. | 20=0 | B. | $\sqrt{4}$=±2 | C. | 2-1=$\frac{1}{2}$ | D. | 23=6 |
15.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (a+b)2=a2+b2 | C. | (-a)3=-6a3 | D. | -(x-2)=2-x |
2.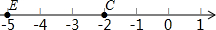 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
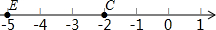 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )| A. | 26 | B. | 27 | C. | 28 | D. | 29 |
19.下列运算正确的是( )
| A. | a4÷a2=a2 | B. | (a+b)(a+b)=a2+b2 | C. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ | D. | (-$\frac{1}{2}$)-2=-4 |
16.下列计算正确的是( )
| A. | 3a2-a2=3 | B. | a2•a4=a8 | C. | (a3)2=a6 | D. | a6÷a2=a3 |
17.一组数据1,0,-1,2,3的中位数是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |