题目内容
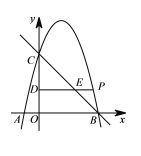
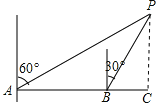
【题目】如图，一艘轮船在
处测得灯塔
位于其北偏东
方向上，轮船沿正东方向航行20海里到达
处后，测得灯塔位于其北偏东
方向上，轮船沿计划路线航行时与灯塔的距离最少是_______海里.（结果保留根号）
【答案】
【解析】
过点P作PC⊥AB，交AB的延长线于点C，由∠PAC和∠PBC的正切值得到PC的两种表示方法，从而得到方程，再根据AB=20海里求出BC，继而可以算出最短距离PC的值.
解：如图，过点P作PC⊥AB，交AB的延长线于点C，
由题意可知：∠PAC=30°，∠PBC=60°，AB=20，
∴tan∠PAC=
=
，tan∠PBC=
=
，
∴PC=AC=BC，
∴（AB+BC）=BC，
∴（20+BC）=BC，
解得：BC=10，
∴PC=tan∠PBC×BC=，
即轮船沿计划路线航行时与灯塔
的距离最少是PC的长，即海里.
练习册系列答案
相关题目
【题目】某校为了解全校学生假期主题阅读的情况（要求每名学生的文章阅读篇数，最少3篇，最多7篇），随机抽查了部分学生在某一周主题阅读文章的篇数，并制成下列统计图表．
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数（篇） | 3 | 4 | 5 | 6 | 7 |
人数（人） | 20 | 28 |
| 16 | 12 |
请根据统计图表中的信息，解答下列问题：
（1）求被抽查的学生人数和
的值；
（2）求本次抽查的学生文章阅读篇数的中位数和众数；
（3）若该校共有800名学生，根据抽查结果，估计该校学生读书总数．
