题目内容
【题目】科技改变世界.随着科技的发展，自动化程度越来越高，机器人市场越来越火.某商场购进一批
，
两种品牌的编程机器人，进价分别为每台3000元、4000元.市场调查发现：销售3个品牌机器人和2个品牌机器人，可获利润6000元；销售2个品牌机器人和3个品牌机器人，可获利润6500元.
（1）此商场.两种品牌的编程机器人销售价格分别是多少元？
（2）若商场准备用不多于65000元的资金购进，两种品牌的编程机器人共20个，则至少需要购进品牌的编程机器人多少个？
（3）不考虑其它因素，商场打算品牌编程机器人数量不多于品牌编程机器人数量的
，现打算购进，两种品牌编程机器人共40个，怎样进货才能获得最大的利润？
【答案】（1）商场
、
两种品牌的编程机器人销售价格分别是4000元、5500元；（2）至少为15个；（3）购进品牌编程机器人27个，品牌编程机器人13个能获得最大的利润.
【解析】
（1）设商场、两种品牌的编程机器人销售价格分别是
元、
元，根据题意列出方程组，解之即可；
（2）设需要购进品牌的编程机器人
个，根据商场准备用不多于65000元的资金购进，两种品牌的编程机器人共20个列出不等式，求解；
（3）设需要购进品牌的编程机器人
个.利润为
元，得出和b的关系式，再根据品牌编程机器人数量不多于品牌编程机器人数量的
求出b的取值范围，从而求出当b=13时，获得最大利润.
解：（1）设商场、两种品牌的编程机器人销售价格分别是元、元.
根据题意列方程组得：
，
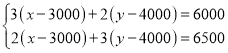解得：
，
答：此商场A，B两种品牌的编程机器人销售价格分别是4000元，5500元.
（2）设需要购进品牌的编程机器人个.
根据题意得： 
解得：
∵为编程机器人的个数
∴为的整数
∴至少为15个
答：至少需要购进品牌的编程机器人15个.
（3）设需要购进品牌的编程机器人个.利润为元.
根据题意得：
根据题意得： 
解得：
∵
∴随的增大而增大
∴当最大时最大
∴的最大整数
∴
则
答：购进品牌编程机器人27个，品牌编程机器人13个能获得最大的利润.
