Question

【题目】如图，在矩形中，，，点为边上点，沿折叠，点在矩形内部的对应点为，若点到矩形两条较长边的距离之比为，则的长为____．

Answer 1

【答案】或或

【解析】

由点到矩形两条较长边的距离之比为分点E在矩形内部，EM：EN=1：4，或EM：EN=4：1，点E在矩形外部，EN：EM=1：4，三种情况讨论，根据折叠的性质和勾股定理可求AP的长度．

解：过点E作ME⊥AD，延长ME交BC与N，

∵四边形ABCD是矩形，

∴AD∥BC，且ME⊥DA，

∴EN⊥BC且∠A=90°=∠ABC=90°，

∴四边形ABNM是矩形，

∴MN=AB=5，AM=BN，

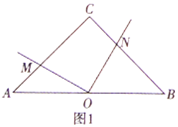
若ME：EN=1：4，如图1，

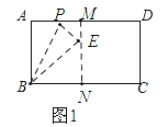
∵ME：EN=1：4,MN=5

∴ME=1,EN=4

∵BE=AB=5,AP=PE

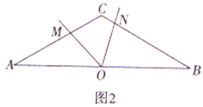
若ME：EN=4：1，则EN=1，ME=4，如图2

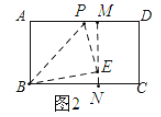
在Rt△BEN中，BN=

∴

在Rt△PME中，

解得

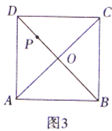
若点E在矩形外，如图3

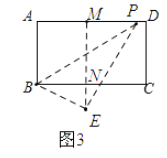
∵EN：EM=1：4

∴

在Rt△BEN中，

∴

在Rt△PME中，

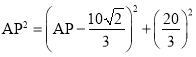
解得：

故答案为:或或