题目内容
6.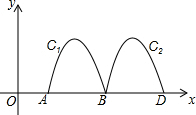 如图,抛物线y=-2x2+8x-6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是-3<m<-$\frac{15}{8}$.
如图,抛物线y=-2x2+8x-6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是-3<m<-$\frac{15}{8}$.
分析 首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=x+m与抛物线C2相切时m的值以及直线y=x+m过点B时m的值,结合图形即可得到答案.
解答 解:令y=-2x2+8x-6=0,
即x2-4x+3=0,
解得x=1或3,
则点A(1,0),B(3,0),
由于将C1向右平移2个长度单位得C2,
则C2解析式为y=-2(x-4)2+2(3≤x≤5),
当y=x+m1与C2相切时,
令y=x+m1=y=-2(x-4)2+2,
即2x2-15x+30+m1=0,
△=-8m1-15=0,
解得m1=-$\frac{15}{8}$,
当y=x+m2过点B时,
即0=3+m2,
m2=-3,
当-3<m<-$\frac{15}{8}$时直线y=x+m与C1、C2共有3个不同的交点,
故答案是:-3<m<-$\frac{15}{8}$.
点评 本题主要考查抛物线与x轴交点以及二次函数图象与几何变换的知识,解答本题的关键是正确地画出图形,利用数形结合进行解题,此题有一定的难度.

练习册系列答案
相关题目
14.从北京到济南中间共有4个站点,则北京到济南之间共有( )种车票.
| A. | 15 | B. | 6 | C. | 30 | D. | 20 |
11.如果|x|=5,那么x等于( )
| A. | 5 | B. | -5 | C. | +5或-5 | D. | 以上都不对 |
18.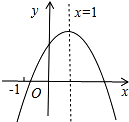 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),
其中正确的结论有( )
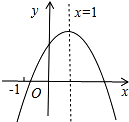 已知二次函数y=ax2+bx+c的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的实数),
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知点P1(a,2013)和P2(-2012,b)关于原点对称,则(a+b)2014的值为( )
| A. | 1 | B. | -1 | C. | 72014 | D. | -72014 |
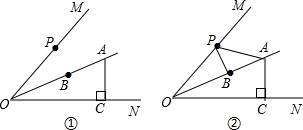
 如图,AE=AD,AB=AC,BD=EC,BE=6,AD=4,则AC=10.
如图,AE=AD,AB=AC,BD=EC,BE=6,AD=4,则AC=10.