题目内容
1. 如图,AE=AD,AB=AC,BD=EC,BE=6,AD=4,则AC=10.
如图,AE=AD,AB=AC,BD=EC,BE=6,AD=4,则AC=10.
分析 根据AE=AD,AB=AC,利用等式的性质:AB-AE=AC-AD,得到BE=CD,再根据AC=AD+CD即可解答.
解答 解:∵AE=AD,AB=AC,
∴AB-AE=AC-AD,
即BE=CD,
∵BE=6,
∴CD=6,
∴AC=AD+CD=6+4=10.
故答案为:10.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是由AE=AD,AB=AC,得到AB-AE=AC-AD,即BE=CD.

练习册系列答案
相关题目
9.阅读下列材料:如果(x+1)2-9=0,那么(x+1)2-32=(x+1+3)(x+1-3)=(x+4)(x-2),则(x+4)(x-2)=0,由此可知:x1=-4,x2=2.根据以上材料计算x2-2x-1=0的根为( )
| A. | x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | B. | x1=-1+$\sqrt{2}$,x2=11-$\sqrt{2}$ | C. | x1=-1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | D. | x1=1+$\sqrt{2}$,x2=-1-$\sqrt{2}$ |
10.下列命题错误的是( )
| A. | 两个相似三角形的对应角相等,对应值成比例 | |
| B. | 两个全等三角形一定相似 | |
| C. | 两个等腰三角形一定是相似 | |
| D. | 相似的两个三角形不一定全等 |
11.甲、乙两台机床同时加工直径为10mm的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取5件进行检测,结果如下(单位:mm):
(1)分别求出这两台机床所加工零件直径的平均数、极差和方差;
(2)哪一台机床生产零件的稳定性更好一些?为什么?
| 甲 | 10 | 9.8 | 10 | 10.2 | 10 |
| 乙 | 9.9 | 10 | 10 | 10.1 | 10 |
(2)哪一台机床生产零件的稳定性更好一些?为什么?
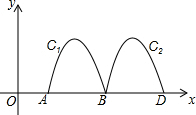 如图,抛物线y=-2x2+8x-6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是-3<m<-$\frac{15}{8}$.
如图,抛物线y=-2x2+8x-6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是-3<m<-$\frac{15}{8}$.