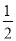题目内容

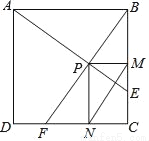
如图，在边长为1的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），过点P作PM∥CD交BC于M点，PN∥BC交CD于N点，连接MN，在运动过程中，则下列结论：①△ABE≌△BCF；②AE=BF；③AE⊥BF；④CF2=PE•BF；⑤线段MN的最小值为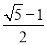．其中正确的结论有（　　）

A. 2个 B. 3个 C. 4个 D. 5个

D 【解析】试题分析：如图， ∵动点F，E的速度相同， ∴DF＝CE， 又∵CD＝BC， ∴CF＝BE， 在△ABE和△BCF中， ， ∴△ABE≌△BCF（SAS），故①正确； ∴∠BAE＝∠CBF，AE＝BF，故②正确； ∵∠BAE＋∠BEA＝90°， ∴∠CBF＋∠BEA＝90°， ∴∠APB＝90°，故③正确； ...
练习册系列答案
相关题目

小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后，发现下端刚好接触地面，则旗杆的高是( )．

A. 8米 B. 10米 C. 12米 D. 14米

C 【解析】 画出示意图如下所示： 设旗杆的高AB为xm,则绳子AC的长为(x+1)m， 在Rt△ABC中,AB2+BC2=AC2， ∴x2+52=(x+1)2， 解得：x=12， ∴AB=12m， 即旗杆的高是12m. 故选D.

8 =2x÷2，则 x =________；

4 【解析】试题解析：因为23=8 ，2x÷2=2x-1，则x-1=3 ，故x=4. 故答案为：4.

如图，△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD、DE．

（1）求证：D是BC的中点；

（2）若DE=3，BD﹣AD=2，求⊙O的半径；

（3）在（2）的条件下，求弦AE的长．

（1）证明见解析；（2）⊙O的半径为；（3）AE=． 【解析】试题分析：（1）根据直径所对的圆周角是直角得到AD⊥BC，应用等腰三角形的三线合一证得点D为BC的中点； （2）应用等腰三角形的性质和判定证得BD=DE=3，进而求得BD=3，AD=1，应用勾股定理求得AB的长，即可得到半径的长； （3）解法一：通过证明△CAB∽△CDE，应用相似三角形的性质解得CE的长，再求AE的长...

如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8cm，DC=2cm，则OC=_____cm．

5 【解析】试题分析：连接OA，∵OC⊥AB，∴AD=AB=4cm，设⊙O的半径为R，由勾股定理得，OA2=AD2+OD2，∴R2=42+（R﹣2）2，解得R=5，∴OC=5cm．故答案为：5．

（2017四川省巴中市）下列说法正确的是（　　）

A. “打开电视机，正在播放体育节目”是必然事件

B. 了解夏季冷饮市场上冰淇淋的质量情况适合用普查

C. 抛掷一枚普通硬币，“这枚硬币正面朝上”，这一事件发生的概率为

D. 甲、乙两人在相同条件下各射击10次，他们的成绩的平均数相同，方差分别是S甲2=0.3，S乙2=0.5，则乙的射击成绩较稳定

C 【解析】试题分析：A、“打开电视机，正在播放体育节目”是随机事件，故此选项错误； B、了解夏季冷饮市场上冰淇淋的质量情况应该采用抽样调查的方式，故此选项错误； C、抛掷一枚普通硬币，“这枚硬币正面朝上”，这一事件发生的概率为，故此选项正确； D、甲、乙两人在相同条件下各射击10次，他们的成绩的平均数相同，方差分别是S甲2＝0.3，S乙2＝0.5，S甲2＜S乙2，所以甲的...

如图，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD，BF，若两个正方形的边长满足a＋b＝10，ab＝20，你能求出阴影部分的面积吗？

20 【解析】分析：阴影部分面积等于两个正方形面积之和减去两个直角三角形面积,求出即可. 本题解析： S＝a2＋b2－a2－ (a＋b)b＝a2＋b2－a2－ab－b2＝ (a2－ab＋b2)＝ [(a＋b)2－3ab]，当a＋b＝10，ab＝20时，S＝ [102－3×20]＝20

下列各图中的直线都相交于一点.

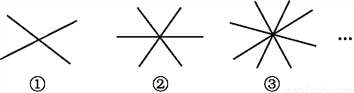
(1)请观察上图并填下表:

图形编号

①

②

③

…

对顶角的对数

…

(2)若n条直线相交于一点,则共有多少对对顶角?

(1)2;6;12；(2)对顶角共有n(n-1)对. 【解析】试题分析：根据对顶角的定义和邻补角的定义分别计算对数即可． 试题解析：①对顶角有2对，邻补角有4对； ②对顶角有6对，邻补角12对； ③对顶角有12对，邻补角有24对； n条直线相交于一点，共有n（n-1）对对顶角．

如图，在△ABC中，∠C＝90°，AC＝3，点P是边BC上的动点，则AP的长不可能是( )

A. 5 B. 4 C. 3 D. 2.5

D 【解析】试题解析：已知，在△ABC中，∠C=90°，AC=3， 根据垂线段最短，可知AP的长不可小于3，当P和C重合时，AP=3， 故选D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网