题目内容
20. 如图,已知Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,值△PDE内作第二个内接正方形HIKJ;再取线段JK的中点Q,在△QHI内作第三个内接正方形;…依次进行下去,则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$(n为正整数).
如图,已知Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,值△PDE内作第二个内接正方形HIKJ;再取线段JK的中点Q,在△QHI内作第三个内接正方形;…依次进行下去,则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$(n为正整数).
分析 首先根据勾股定理得出BC的长,进而利用等腰直角三角形的性质得出DE的长,再利用锐角三角函数的关系得出$\frac{EI}{KI}$=$\frac{PF}{EF}$=$\frac{1}{2}$,即可得出正方形边长之间的变化规律,得出答案即可.
解答 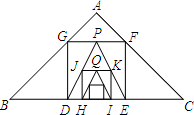 解:∵在Rt△ABC中,AB=AC=3$\sqrt{2}$,
解:∵在Rt△ABC中,AB=AC=3$\sqrt{2}$,
∴∠B=∠C=45°,BC=6,
∵在△ABC内作第一个内接正方形DEFG;
∴EF=EC=DG=BD,
∴DE=$\frac{1}{3}$BC,
∴DE=2,
∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,
∴$\frac{EI}{KI}$=$\frac{PF}{EF}$=$\frac{1}{2}$,
∴EI=$\frac{1}{2}$KI=$\frac{1}{2}$HI,
∵DH=EI,
∴HI=$\frac{1}{2}$DE=($\frac{1}{2}$)2-1×2,
第n个内接正方形的边长为:2×($\frac{1}{2}$)n-1,
则第n个内接正方形的面积为$\frac{1}{{4}^{n-2}}$.
故答案为:$\frac{1}{{4}^{n-2}}$.
点评 此题主要考查了正方形的性质以及数字变化规律和勾股定理等知识,根据已知得出正方形边长的变化规律是解题关键.

练习册系列答案
相关题目
15.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.某乡有四个村生产草莓,每千克售2.25元.填表:(用计算器计算)
| 村别 | 甲村 | 乙村 | 丙村 | 丁村 | 四村合计 |
| 数量(kg) | 12560 | 8974 | 9670 | 8796 | 40000 |
| 金额(元) | 28260 | 20191.5 | 21757.5 | 19791 | 90000 |
 如图所示,F,G是0A上两点,M、N是0B上两点,且FG=MN,△PFG的面积和△PMN的面积相等.求证:0P平分∠A.
如图所示,F,G是0A上两点,M、N是0B上两点,且FG=MN,△PFG的面积和△PMN的面积相等.求证:0P平分∠A.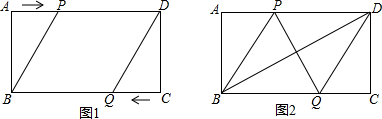
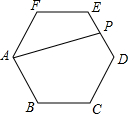 如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,求AP的长.
如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,求AP的长.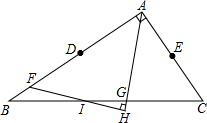 已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.