题目内容
4.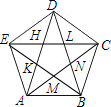 已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,
已知:如图,连结正五边形ABCDE各条对角线,就得到一个五角星图案,(1)求五角星的各个顶角(如∠ADB)的度数;
(2)求证:五边形MNLHK是正五边形.
分析 (1)先求得正五边形的内角和,从而得出每一个内角的度数;
(2)求证各个角的度数,再求得各边的长度,即可得出结论.
解答 解:(1)∵五边形ABCDE是正五边形,
∴∠ABC=(5-2)×180°×$\frac{1}{5}$=108°,
∴∠ADB=108°-$\frac{1}{2}$(180°-108°)=72°;
(2)证明:∵∠ABE=∠CBD=36°,
∴∠DBE=36°,
同理∠KMN=∠MNL=∠NLH=∠LHK=∠HKM,
△AMK≌△BMN≌△CNL≌△DHL≌△EHK,
∴MN=NL=LH=HK=MK,
∴五边形MNLHK是正五边形.
点评 本题考查了正多边形和圆,以及多边形的内角和公式和正多边形的判定,掌握判定方法是解题的关键.

练习册系列答案
相关题目
15.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
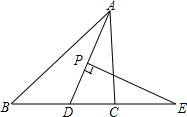 如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.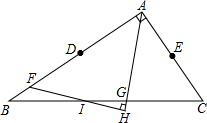 已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.