题目内容
5.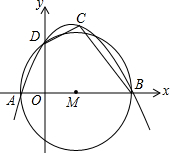 如图,⊙M的圆心M在x轴上,且与x轴分别交于A、B两点与y轴的正半轴交于点D,点A、B的横坐标分别是方程x2=3x+4的两根,一条抛物线经过A、B、D三点,点C为第一象限抛物线上一动点.
如图,⊙M的圆心M在x轴上,且与x轴分别交于A、B两点与y轴的正半轴交于点D,点A、B的横坐标分别是方程x2=3x+4的两根,一条抛物线经过A、B、D三点,点C为第一象限抛物线上一动点.(1)求此抛物线的解析式;
(2)求四边形ABCD面积的最大值.
分析 (1)A(-1,0),B(4,0),可以假设抛物线为y=a(x+1)(x-4),连接BD,由△AOD∽△DOB,得OD2=AO•BO,推出OD=2,推出D(0,2),把D(0,2)代入y=a(x+1)(x-4)中,求出a即可.
(2)设四边形ABCD面积为S,构建二次函数,利用二次函数的性质解决问题即可.
解答 解:(1)∵点A、B的横坐标分别是方程x2=3x+4的两根,
∴A(-1,0),B(4,0),
可以假设抛物线为y=a(x+1)(x-4),连接BD,
∵AB是直径,
∴∠ADB=90°,
∵DO⊥AB,
∴∠AOD=∠DOB=90°,
∵∠ADO+∠DAO=90°,∠ADO+∠ODB=90°,
∴∠DAO=∠BDO,
∴△AOD∽△DOB,
∴OD2=AO•BO,
∴OD=2,
∴D(0,2),
把D(0,2)代入y=a(x+1)(x-4)中,得到a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)连接OC.设C(m,-$\frac{1}{2}$m2+$\frac{3}{2}$m+2),
S=S△ADO+S△DCO+S△BCO=$\frac{1}{2}$×1×2+$\frac{1}{2}$×2×m+$\frac{1}{2}$×4×(-$\frac{1}{2}$m2+$\frac{3}{2}$m+2)=-(m-2)2+9,
∵-1<0,
∴m=2时,S有最大值,最大值为9.
点评 本题考查二次函数与x轴的交点、二次函数的最值问题、待定系数法等知识,解题的关键是学会根据二次函数解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
15. 如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )
如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )
 如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )
如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )| A. | a<b | B. | |a|>|b| | C. | a+b>0 | D. | ab<0 |
20.在多项式-12ab3c-8a3b中应提取的公因式是( )
| A. | 4ab2 | B. | -4abc | C. | -4ab2 | D. | -4ab |
14.若a2+a-1=0,则a3+2a2+2016的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
15.能清楚地表示出各部分在总体中所占百分比的统计图是( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 都可以 |
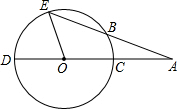 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.