题目内容
18. 如图,在△ABC中,∠C=90°,∠A=30°,点D,E分别在AC,AB边上,沿DE折叠使点A落在BC上的点F处,且EF⊥BC,BE=4,则CF=$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠A=30°,点D,E分别在AC,AB边上,沿DE折叠使点A落在BC上的点F处,且EF⊥BC,BE=4,则CF=$\sqrt{3}$.
分析 在Rt△BEF中,求出EF、BF,根据翻折不变性,可知AE=EF,求出AB,根据BC=$\frac{1}{2}$AB,求出BC即可解决问题.
解答 解:∵EF⊥BC,
∴∠C=∠EFB=90°,
∴EF∥AC,
∴∠BEF=∠A=30°,
∵BE=4,
∴BF=$\frac{1}{2}$BE=2,EF=$\sqrt{3}$BF=2$\sqrt{3}$,
由折叠性质可知AE=EF=2$\sqrt{3}$,
∴AB=2$\sqrt{3}$+4,
∵BC=$\frac{1}{2}$AB=$\sqrt{3}$+2,
∴CF=BC-BF=$\sqrt{3}$+2-2=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 本题考查翻折变换、直角三角形30度角性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下面两个数互为相反数的是( )
| A. | -(+9)与+(-9) | B. | -0.5与-(+0.5) | C. | -1.25与$\frac{4}{5}$ | D. | +(-0.01)与-(-$\frac{1}{100}$) |
3.计算4-2的结果是( )
| A. | -16 | B. | -$\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | -$\frac{1}{16}$ |
8.下列比较大小正确的是( )
| A. | -12>-11 | B. | |-6|=-(-6) | C. | -(-31)<+(-31) | D. | -$\frac{1}{16}$>0 |
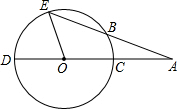 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°. 如图,平面直角坐标系中,长方形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB,AB于点D,E.若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).
如图,平面直角坐标系中,长方形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB,AB于点D,E.若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).