题目内容
一串数排成一行,它们的规律是这样的:头两个数都是l,从第三个数开始,每一个数都是前两个数的和,也就是1,1,2,3,5,8,13,21,34,55…,问:这串数的前100个数中(包括第100个数),有多少个偶数?
考点:规律型:数字的变化类
专题:规律型
分析:从数列:1,1,2,3,5,8,13,21,34,55,89,…可以得出规律,每两个奇数之后为一个偶数,则这串数前100个数(包括第100个数)中偶数的个数为:
取整数部分.
| 100 |
| 3 |
解答:解:从数列中可以得到规律每两个奇数之后为一个偶数,
其中前100个数(包括第100个数)中偶数的个数为
=33…1,
故这串数前100个数中有33个偶数.
其中前100个数(包括第100个数)中偶数的个数为
| 100 |
| 3 |
故这串数前100个数中有33个偶数.
点评:本题考查了同学对所给数列的存在方式找出其具有一定规律的能力.解题关键是发现每三个连续数中恰有一个偶数.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
人均住房面积与住房总面积、人口总数有关.某城市人口总数为50万,人均住房面积为30m2,现人口每年以2%增加,人均住房面积以5%增加,则每年住房总面积增长( )
| A、2% | B、5% |
| C、10% | D、7.1% |
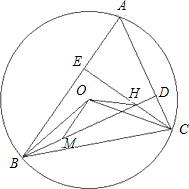 如图,⊙O为△ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH.
如图,⊙O为△ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH.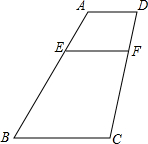 如图,梯形ABCD中,AD∥BC,E为线段AB上的点,且满足AE=AD,BE=BC,过E作EF∥BC交CD于F,设P为线段CD上任意一点,试说明
如图,梯形ABCD中,AD∥BC,E为线段AB上的点,且满足AE=AD,BE=BC,过E作EF∥BC交CD于F,设P为线段CD上任意一点,试说明 将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于
将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于 如图,F、G、H分别是平行四边形ABCD的边BC、CD、AD上的三等分点,E是AB边的中点,已知四边形EFGH的面积是51平方厘米,那么平行四边形ABCD的面积是
如图,F、G、H分别是平行四边形ABCD的边BC、CD、AD上的三等分点,E是AB边的中点,已知四边形EFGH的面积是51平方厘米,那么平行四边形ABCD的面积是