题目内容
7.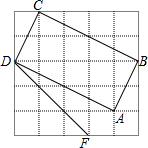 (1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由.
(1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由.(2)以DE为一边作一个矩形,要求另外两个顶点也在方格顶点上.
分析 (1)由勾股定理求出AB=CD,AD=BC,得出四边形ABCD是平行四边形,由勾股定理的逆定理证出∠BAD=90°,即可得出结论;
(2)由(1)中的矩形容易画出以DE为一边的矩形.
解答 解:(1)四边形ABCD是矩形;理由如下:
由勾股定理得:AB=CD=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AD=BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴四边形ABCD是平行四边形,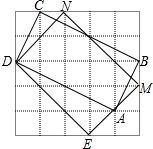
∵AB2+AD2=25,BD2=25,
∴AB2+AD2=BD2,
∴△ABD是直角三角形,∠BAD=90°,
∴四边形ABCD是矩形;
(2)如图2所示,
四边形DEMN即为所求.
点评 本题考查了矩形的判定与性质、作图、勾股定理、勾股定理的逆定理;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算与作图是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
12.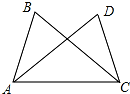 如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )
如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )
 如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )
如图,已知AB=CD,那么添加下列条件后,仍不能说明△ABC≌△CDA的是( )| A. | ∠BAC=∠DCA | B. | BC=DA | C. | ∠D=∠B=90° | D. | ∠BAC=∠DAC |
17.运动会前夕,为了提高体能,小明每天放学回家做仰卧起坐.他制作了一张表格记录自己每天做仰卧起坐的成绩.以每分钟做40个为标准,超过的个数记为正,不足的个数记为负.下表是小明一周做仰卧起坐的记录:
根据上述记录表,回答下列问题:
(1)小明这周一天最多做54个,最少做30个;
(2)这周小明平均每天做多少个?
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 个数 | +14 | +8 | -5 | +2 | -10 | +1 | -3 |
(1)小明这周一天最多做54个,最少做30个;
(2)这周小明平均每天做多少个?
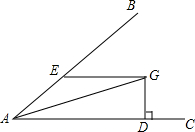 已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG.
已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG. 如图,在钝角△ABC中.
如图,在钝角△ABC中. 如图,在△ABC中,AB=AC=10,BC=12,点P是AC边上的一个动点,当点P在AC边上移动时,BP为最小值时,PC的长是$\frac{36}{5}$.
如图,在△ABC中,AB=AC=10,BC=12,点P是AC边上的一个动点,当点P在AC边上移动时,BP为最小值时,PC的长是$\frac{36}{5}$.