题目内容
18.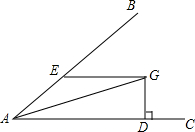 已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG.
已知:如图,∠BAC=30°,G为∠BAC平分线上一点,EG∥AC,EG交AB于点E;GD⊥AC,垂足为点D.求证:GD=$\frac{1}{2}$EG.
分析 作辅助线GF⊥AB,根据角平分线的性质可知GF=GD,由EG∥AC可知∠2=∠EGA,从而推出∠3与∠BAC的关系,从而得出GE与GF的关系,进而得到GE与GD的关系.
解答 证明:如下图所示:作GF⊥AB于点F,
∵AG为∠BAC平分线,GF⊥AB,GD⊥AC,
∴∠1=∠2,GF=GD.
∵EG∥AC,
∴∠2=∠EGA.
∴∠1+∠EGA=∠1+∠2=∠BAC.
∵∠BAC=30°,∠3=∠1+∠EGA,
∴∠3=30°.
∵GF⊥AB,
∴GE=2GF.
又∵GF=GD,
∴GE=2GD.
即$GD=\frac{1}{2}GE$.
点评 本题考查角平分线的性质角、平行线的性质和在直角三角形中30°角所对的直角边与斜边的关系,关键是正确分析题目,灵活变化最终求得结论成立.

练习册系列答案
相关题目
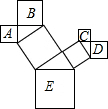 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
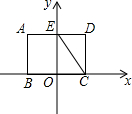 以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.
以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.



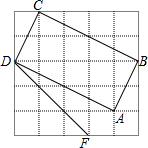 (1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由.
(1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由.