题目内容
19.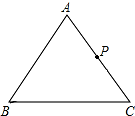 如图,在△ABC中,AB=AC=10,BC=12,点P是AC边上的一个动点,当点P在AC边上移动时,BP为最小值时,PC的长是$\frac{36}{5}$.
如图,在△ABC中,AB=AC=10,BC=12,点P是AC边上的一个动点,当点P在AC边上移动时,BP为最小值时,PC的长是$\frac{36}{5}$.
分析 作AD⊥BC于D,则∠ADB=90°,由等腰三角形的性质和勾股定理求出AD,当BP⊥AC时,BP最小;由△ABC的面积的计算方法求出BP的最小值,再由勾股定理求出PC即可.
解答 解:作AD⊥BC于D,如图所示: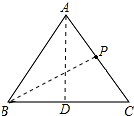
则∠ADB=90°,
∵AB=AC,
∴BD=$\frac{1}{2}$BC=6,
由勾股定理得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
当BP⊥AC时,BP最小,
此时,∠BPC=90°,
∵△ABC的面积=$\frac{1}{2}$AC•BP=$\frac{1}{2}$BC•AD,
即$\frac{1}{2}$×10×BP=$\frac{1}{2}$×12×8,
解得:BP=$\frac{48}{5}$,
∴PC=$\sqrt{B{C}^{2}-B{P}^{2}}$=$\sqrt{1{2}^{2}-(\frac{48}{5})^{2}}$=$\frac{36}{5}$;
故答案为:$\frac{36}{5}$.
点评 本题考查了勾股定理、等腰三角形的性质、垂线段最短、三角形面积的计算方法;熟练掌握勾股定理,由三角形面积的计算方法求出BP的最小值是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4.已知4个数中:(-1)2015,|-2|,-(-1.2),-32,其中正数的个数有( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
9.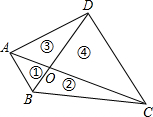 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
 如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )| A. | ①②相似 | B. | ①③相似 | C. | ①④相似 | D. | ②相似 |
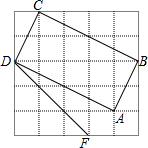 (1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由.
(1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由. 如图,将一块正方形的纸片沿虚线折叠两次,然后沿虚线剪掉一角,最后将剩余部分展开,得到的图案是( )
如图,将一块正方形的纸片沿虚线折叠两次,然后沿虚线剪掉一角,最后将剩余部分展开,得到的图案是( )


