题目内容
2.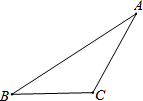 如图,在钝角△ABC中.
如图,在钝角△ABC中.(1)作钝角△ABC的高AM,CN;
(2)若CN=3,AM=6,求BC与AB之比.
分析 (1)过点A作AM⊥BC于M,过点C作CN⊥AB于N,则AM、BN为△ABC的高;
(2)根据三角形面积公式得到$\frac{1}{2}$AM•BC=$\frac{1}{2}$CN•AB,然后利用比例性质求BC与AB的比值.
解答 解:(1)如图,AM、CN为所作;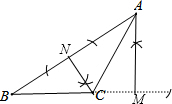
(2)∵AM、BN为△ABC的高,
∴S△ABC=$\frac{1}{2}$AM•BC=$\frac{1}{2}$CN•AB,
∴$\frac{BC}{AB}$=$\frac{CN}{AM}$=$\frac{3}{6}$=$\frac{1}{2}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形面积公式.

练习册系列答案
相关题目
17.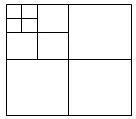 如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…
如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…
(1)填表
(2)若剪n次,共剪出多少个小正方形?
(3)若剪去10次,共剪出多少个小正方形?
(4)若原来正方形的边长为a,求当n=5时,所剪得的所有正方形的周长的和.
 如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…
如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…(1)填表
| 剪的次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 | 10 | 13 | … |
(3)若剪去10次,共剪出多少个小正方形?
(4)若原来正方形的边长为a,求当n=5时,所剪得的所有正方形的周长的和.
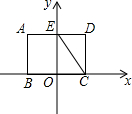 以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.
以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.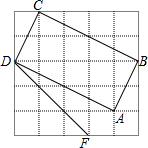 (1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由.
(1)判断如图5×5方格内四边形ABCD是不是矩形,请说明理由. 如图,将一块正方形的纸片沿虚线折叠两次,然后沿虚线剪掉一角,最后将剩余部分展开,得到的图案是( )
如图,将一块正方形的纸片沿虚线折叠两次,然后沿虚线剪掉一角,最后将剩余部分展开,得到的图案是( )


