题目内容
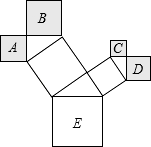
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若 正方形 A、B、C、D 的边长分别是 3、5、2、3,则最大正方形 E 的面积是 .
47【考点】勾股定理.
【分析】分别设中间两个正方形和最大正方形的边长为 x,y,z,由勾股定理得出 x2=32+52,y2=22+32, z2=x2+y2,即最大正方形的面积为 z2.
【解答】解:设中间两个正方形的边长分别为 x、y,最大正方形 E 的边长为 z,则由勾股定理得: x2=32+52=34;
y2=22+32=13;
z2=x2+y2=47;
即最大正方形 E 的边长为: ,所以面积为:z2=47. 故答案为:47.
,所以面积为:z2=47. 故答案为:47.
【点评】本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等 于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目

 .
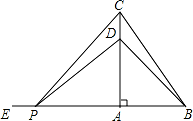
.
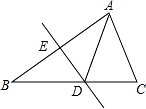
 AC,D、E 分别为 AC、AB 的中点,求 DE 的 长.
AC,D、E 分别为 AC、AB 的中点,求 DE 的 长.
 .
.