题目内容
如图将 4 个长、宽分别均为 a、b 的长方形,摆成了一个大的正方形.利用面积的不同表示方法 写出一个代数恒等式是 .

(a+b)2﹣(a﹣b)2=4ab【考点】完全平方公式的几何背景.
【专题】计算题.
【分析】通过观察可以得大正方形边长为 a+b,小正方形边长为 a﹣b,利用大正方形面积减去小正 方形面积即为阴影部分面积,得出答案.
【解答】解:观察图形得: 大正方形边长为:a+b, 小正方形边长为:a﹣b,
根据大正方形面积﹣小正方形面积=阴影面积得:
(a+b)2﹣(a﹣b)2=4ab. 故答案为:(a+b)2﹣(a﹣b)2=4ab.
【点评】题目考查了完全平方公式的几何背景,学生需要掌握完全平方公式和几何图形的关系即 可.题目整体涉及很好,可以考查学生的观察能力.

练习册系列答案
相关题目
 C.0 D.﹣1
C.0 D.﹣1
 A.﹣1 B.3.1415 C.
A.﹣1 B.3.1415 C.  D.
D.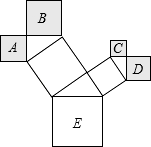

 (B)
(B)
 (D)
(D)