��Ŀ����
��ͼ������ABC �У���BAC=90�㣬AB=6cm��BC=10cm���� D ���߶� AC �ϣ��� CD=2cm���� �� P �� BA ���ӳ����Ͼ� A �� 10cm �� E ���������ÿ�� 2cm ���ٶ������� EA �ķ����˶��� t �룮
��1���� AD �ij���
ֱ��д���ú��� t �Ĵ���ʽ��ʾ PE= 2t ��
��3�����˶������У��Ƿ����ij��ʱ�̣�ʹ��ABC ����ADP ȫ�ȣ������ڣ������ t ֵ�������� �ڣ���˵�����ɣ�
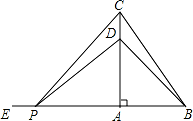
�����㡿ȫ�������ε��ж������ʣ�
��ר�⡿�����ͣ�
����������1�����ݹ��ɶ����õ� AC= =6cm�����ǵõ����ۣ�
=6cm�����ǵõ����ۣ�
���� P �� BA ���ӳ����Ͼ� A �� 10cm �� E ���������ÿ�� 2cm ���ٶ������� EA �ķ����˶��� t
�룬������� PE=2t��
��3�����������������ABC�ա�ADP ʱ��AP=AC=8cm���õ� PE=10��8=2 cm��������� t=1����
��ABC�ա�APD ʱ��AP=AB=6 cm���õ� PE=10��6=4 cm�����ǵõ� t=4��
����𡿽⣺��1���ߡ�BAC=90�㣬AB=6cm��BC=10cm��
��AC=  =6cm��
=6cm��
��CD=2cm��
��AD=6cm��
������ P �� BA ���ӳ����Ͼ� A �� 10cm �� E ���������ÿ�� 2cm ���ٶ������� EA �ķ����˶���
t �룬
��PE=2t�� �ʴ�Ϊ��2t��
��3�����ڣ� ����ABC�ա�ADP ʱ�� AP=AC=8cm��
��PE=10��8=2 cm��
��t=1��
����ABC�ա�APD ʱ��AP=AB=6 cm��
��PE=10��6=4 cm��
��t=4��

 ��[2������3��2 �£���7����
��[2������3��2 �£���7���� A����1 B��3.1415 C��
A����1 B��3.1415 C��  D��
D��

 x=8����ô x=��4 C����� mx=my����ô x=y D�����|x|=|y|����ô x=y
x=8����ô x=��4 C����� mx=my����ô x=y D�����|x|=|y|����ô x=y