题目内容
5.方程组$\left\{\begin{array}{l}-x+y=3\\-x-y=1\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{-x+y=3①}\\{-x-y=1②}\end{array}\right.$,
①+②得:-2x=4,即x=-2,
①-②得:2y=2,即y=1,
则方程组的解为$\left\{\begin{array}{l}x=-2\\ y=1\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | a2•a4=a8 | B. | $\sqrt{4}$=±2 | C. | $\frac{-x-y}{x-y}$=-1 | D. | a4÷a2=a2 |
13.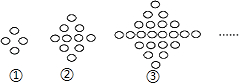 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
 如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )
如图,第①个图形中有4个“○”,第②个图形中有10个“○”,第③个图形中有22个“○”,…,那么第⑤个图形中“○”的个数是( )| A. | 190 | B. | 94 | C. | 70 | D. | 46 |
 如图,直线AB、CD相交于点O,若∠AOD=28°,则∠BOC=28°,∠AOC=152°.
如图,直线AB、CD相交于点O,若∠AOD=28°,则∠BOC=28°,∠AOC=152°. 如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=55°.
如图,在△ABC中,点I是外心,∠BIC=110°,则∠A=55°.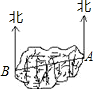 如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏西111°32′.如果A、B两地同时开工,那么在B地按北偏东68°28′方向施工,才能使公路在山腹中准确接通.
如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏西111°32′.如果A、B两地同时开工,那么在B地按北偏东68°28′方向施工,才能使公路在山腹中准确接通.