题目内容
14. 如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为$\sqrt{5}$.
如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为$\sqrt{5}$.
分析 在一次函数y=2x+5中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,由条件可证明△AOB∽△OPB,利用相似三角形的性质可求得OP的长,即可求得EF的最小值.
解答 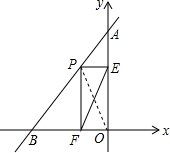 解:∵一次函数y=2x+5中,令x=0,则y=5,令y=0,则x=-$\frac{5}{2}$,
解:∵一次函数y=2x+5中,令x=0,则y=5,令y=0,则x=-$\frac{5}{2}$,
∴A(0,5),B(-$\frac{5}{2}$,0).
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵A(0,5),点B坐标为(-$\frac{5}{2}$,0),
∴OA=5,O B=$\frac{5}{2}$,
由勾股定理得:AB=$\sqrt{{OA}^{2}+{OB}^{2}}$=$\sqrt{{5}^{2}+{(-\frac{5}{2})}^{2}}$=$\frac{5\sqrt{5}}{2}$,
∴AB•OP=OA•OB,
∴OP=$\frac{OA•OB}{AB}$=$\frac{5×\frac{5}{2}}{\frac{5\sqrt{5}}{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
4.有一块长为a,宽为b的长方形铝片,四角各截去一个相同的边长为x的正方形,折起来做成一个无盖的盒子,则此盒子的底面积应为( )
| A. | x2 | B. | (x-a)(b-x) | C. | ab | D. | (a-2x)(b-2x) |
2.若3x=8,3y=4,则3x-y+1的值是( )
| A. | 3 | B. | 5 | C. | 6 | D. | $\frac{2}{3}$ |
19.若函数y=(m2-1)x${\;}^{{m}^{2}-m}$+(m-1)x+1
(1)当m为何值时,该函数为二次函数?
(2)当m为何值时,该函数为一次函数?
(3)该函数可能为反比例函数吗?为什么?
(1)当m为何值时,该函数为二次函数?
(2)当m为何值时,该函数为一次函数?
(3)该函数可能为反比例函数吗?为什么?
6.平行四边形的两邻边分别为6和8,那么其对角线应( )
| A. | 大于2 | B. | 小于14 | C. | 大于2且小于14 | D. | 大于2或小于12 |
6.93号汽油价格上次已按原价降低了b元/升,现在又下调5%,使价格降到a元/升.那么原价格为( )元/升.
| A. | $\frac{19}{20}$a-b | B. | $\frac{20}{19}$a-b | C. | $\frac{19}{20}$a+b | D. | $\frac{20}{19}$a+b |
7.下列各说法一定成立的是( )
| A. | 画直线AB=10厘米 | |
| B. | 已知A、B、C三点,过这三点画一条直线 | |
| C. | 画射线OB=10厘米 | |
| D. | 过直线AB外一点画一条直线和直线AB平行 |