题目内容
10.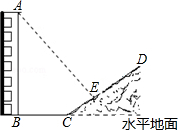 如图,一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长BC=25米,落在坡面上的影长CE=20米,已知小丽测得同一时刻1米高的竹竿在水平地面上的影长为0.8米,求楼房AB的高.($\sqrt{3}$≈1.7)
如图,一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长BC=25米,落在坡面上的影长CE=20米,已知小丽测得同一时刻1米高的竹竿在水平地面上的影长为0.8米,求楼房AB的高.($\sqrt{3}$≈1.7)
分析 延长AE交BC的延长线于F,作EG⊥CF,根据CE=20米,∠ECG=30°,分别求出EG、CG的长度,又根据竹竿在水平面上的影长,可得EG:GF=1:0.8,AB:BF=1:0.8,代入求出BF、AB的长度即可.
解答 解:延长AE交BC的延长线于F,作EG⊥CF,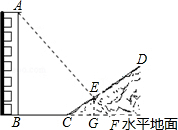
∵CE=20米,∠ECG=30°,
∴EG=10米,CG=10$\sqrt{3}$≈17(米),
又∵$\frac{EG}{GF}=\frac{1}{0.8}$,
∴$\frac{10}{GF}=\frac{1}{0.8}$,
∴GF=8米,
∴BF=25+17+8=50(米),
∵$\frac{AB}{BF}=\frac{1}{0.8}$,
∴$\frac{AB}{50}=\frac{1}{0.8}$,
∴AB=62.5米.
即楼房的高度约为62.5米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题目所给的角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列命题是真命题的是( )
| A. | 四条边都相等的四边形是矩形 | |
| B. | 菱形的对角线相等 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 对角线相等且互相平分的四边形是矩形 |
5.若反比例函数y=$\frac{k-2}{x}$的图象位于第二、四象限,则k的取值可以是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 以上都不是 |
15.如果2是一元二次方程x2=x+c的一个根,那么常数c是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
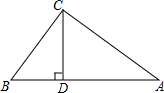 如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}=\frac{CD}{BD}$
如图,△ABC中,CD是边AB上的高,且$\frac{AD}{CD}=\frac{CD}{BD}$ 如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数.